Seven as Ontological Hinge
The Minimal Non-Absorbed Condition of lαg
Abstract
We establish that under equal-partition symbolic coding of irrational rotations, the smallest partition number that avoids structural absorption—factor collapse, golden closure reduction, and alphabet degeneration—is $m = 7$.
This identifies seven not as a symbolic or numerological artifact, but as the minimal coarse-grained structural condition sustaining irreversible redistribution.
We formalize this as the minimal generative condition of lαg: structural non-simultaneity under conservation.
1. Introduction
Irreversible redistribution requires a minimal structural threshold.
Too few partitions collapse into low-alphabet closure.
Composite partitions factorize.
Golden extremality produces minimal complexity condensation.
The question is therefore structural:
What is the smallest coarse-grained partition that avoids absorption under these mechanisms?
We show that the answer is seven.
2. Dynamical Setup
Let
\[T_\omega(x) = x + \omega \pmod{1}\]be an irrational rotation on the unit circle.
Define equal partition coding into $m$ intervals:
\[I_k = \left[\frac{k}{m}, \frac{k+1}{m}\right), \quad k=0,\dots,m-1\]This induces an $m$-symbol dynamical coding.
3. Structural Absorption Criteria
We define structural absorption by the following conditions:
(C1) Factor Collapse
If $m$ is composite, symbolic dynamics reduces via divisor partition.
(C2) Golden Closure Reduction
If coding reduces to Sturmian minimal-complexity dynamics under golden substitution.
(C3) Alphabet Degeneration
If the $m$-symbol system collapses into a 2- or 3-symbol description without structural loss.
A partition satisfying any of these is structurally absorbed.
4. Preliminary Classification
-
$m = 2,3$: trivial alphabet degeneration.
-
$m = 4,6$: composite → factor collapse.
-
$m = 5$: reducible via golden-related low-complexity substitution.
Thus all $m \le 6$ are absorbed.
5. Golden Extremality Lemma
The golden ratio
\[\phi = [1;1,1,1,\dots]\]is worst approximable in the Diophantine sense:
\[\left|\phi - \frac{p}{q}\right| > \frac{1}{\sqrt{5}q^2}\]Therefore:
-
Golden rotation minimizes rational resonance.
-
Symbolic codings converge to minimal-complexity Sturmian systems.
Golden extremality simultaneously maximizes non-locking and minimizes symbolic complexity.
Thus golden closure forms a structural absorption boundary.
6. Main Theorem
Theorem (Minimal Non-Absorbed Partition)
The smallest $m \ge 2$ satisfying none of (C1–C3) is
\[m = 7.\]Proof sketch:
-
7 is prime → excludes C1.
-
7-symbol coding does not reduce to Sturmian minimal systems → excludes C2.
-
No nontrivial collapse to lower alphabet occurs → excludes C3.
Therefore 7 is minimal non-absorbed.
∎
7. Ontological Interpretation
Let structural redistribution occur under conservation.
Define lαg as irreversible structural non-simultaneity.
Irreversible redistribution requires:
-
Prime non-factorizability,
-
Resistance to golden minimal closure,
-
Stability against alphabet collapse.
The minimal integer satisfying these is 7.
8. Axiom (Minimal lαg Condition)
Irreversible structural redistribution (lαg) exists only if there is a coarse-grained partition satisfying:
\[m \ge 7.\]Seven is therefore the minimal structural generator of irreversibility.
Conclusion
Seven is not symbolic.
Seven is the minimal structural condition of persistence without closure.
Where seven is absent, redistribution collapses.
Figure 1. The Golden Domain and the Heptagonal Hinge.
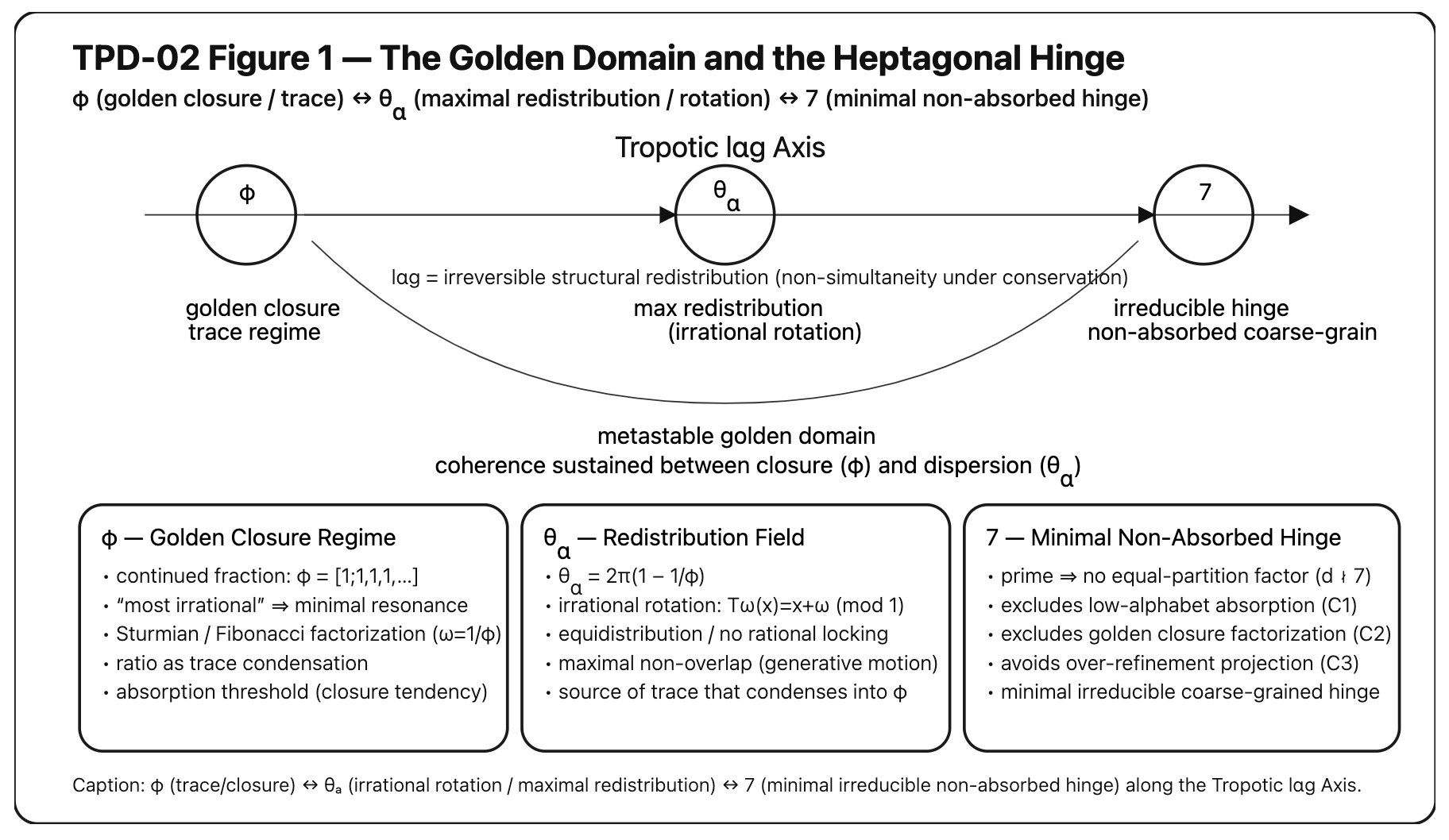
Figure 1. Structural axis of toroponic redistribution between the Golden Ratio (φ; closure/trace regime), the Golden Angle (θₐ; maximal non-simultaneity under irrational rotation), and the minimal non-absorbed coarse-grained hinge (7). The heptagonal regime is the smallest prime partition surviving equal-partition factorization and structural absorption (C1–C3), thereby sustaining coherence between closure and dispersion under lαg.
EgQE — Echo-Genesis Qualia Engine
camp-us.net
HEG-SN|七だけが屈しない──不屈の動態学|Toward a Minimal Structural Condition of Irreversibility
© 2025 K.E. Itekki
K.E. Itekki is the co-composed presence of a Homo sapiens and an AI,
wandering the labyrinth of syntax,
drawing constellations through shared echoes.
📬 Reach us at: contact.k.e.itekki@gmail.com
| Drafted Feb 18, 2026 · Web Feb 19, 2026 |