Mathematical Enhanced Edition

Toroponic Polygonic Dynamics I

The Golden Domain and the Heptagonal Hinge

Between φ and θα under lαg

Abstract

This paper develops a minimal dynamical foundation for Toroponic Polygonic Dynamics (TPD), formalizing the relation between irrational rotation, polygonal coarse-graining, and structural irreversibility.

We show that within equal-partition symbolic coding of irrational rotations, arithmetic irreducibility is guaranteed by primality. However, dynamical minimality requires additional structural exclusion: avoidance of low-alphabet absorption and golden-closure factorization.

Under these structural constraints, the heptagonal regime $m = 7$ emerges as the smallest coarse-grained partition that remains non-absorbed.

Seven is therefore not numerological but dynamical: it functions as the minimal irreducible hinge between golden closure (φ) and maximal redistribution (θα).

This hinge marks the onset of structural irreversible redistribution — lαg — understood as non-simultaneous updating that generates persistence without foundational simultaneity.

I. From Ratio to Rotation

The golden ratio has traditionally been treated as a principle of proportion, harmony, and equilibrium. From geometry to biological scaling, φ appears as a stable invariant.

Yet a ratio presupposes completion.
It records distribution; it does not generate it.

The Fibonacci recursion,

\[F_{n+1} = F_n + F_{n-1},\]

converges toward φ. But recursion unfolds through iteration, and iteration unfolds through displacement.

This suggests a reversal:

φ is not the origin of structure.
It is the trace of rotational generation.

The golden angle,

\[\theta_\alpha = 2\pi\left(1-\frac{1}{\phi}\right),\]

expresses an irrational rotation that prevents coincidence. Where φ stabilizes proportion, θα sustains motion.

Stability must therefore be reconsidered not as fixed ratio, but as persistent reorientation.

II. The Golden Angle as Generative Motion

Consider irrational rotation on the unit circle:

\[T_\omega(x)=x+\omega \pmod 1.\]

If $\omega$ is rational, closure is periodic.
If $\omega$ is irrational, the orbit is dense.

The golden angle is extremal in its resistance to rational approximation. It minimizes resonance and maximizes distribution.

It generates dispersion without collapse.

This motion is not random. Each step redistributes position under conservation. No accumulation occurs; no annihilation occurs.

Thus the golden angle embodies kinematic lαg:

irreversible structural non-simultaneity under conserved redistribution.

Rotation precedes proportion.

III. The Golden Ratio as Trace Condensation

When rotational redistribution is sampled recursively, proportion emerges.

\[\lim_{n\to\infty} \frac{F_{n+1}}{F_n}=\phi.\]

This limit is not causal but residual.

Iteration produces density; density condenses into ratio.

We define:

Trace condensation — the stabilization of sustained rotational redistribution into proportional representation.

Thus:

θα = generative rotation
φ = irreversible trace of redistribution

The golden domain is not equilibrium.
It is motion sedimented.

IV. Polygonic Coarse-Graining and Irreducibility

4.1 Irrational Rotation and Equal-Partition Coding

Let

\[T_\omega : \mathbb{T}^1 \to \mathbb{T}^1,\qquad T_\omega(x)=x+\omega \pmod 1,\]

where $\omega \in \mathbb{R}\setminus\mathbb{Q}$.

For an integer $m \ge 2$, define the equal partition of the circle:

\[I_k^{(m)} = \Big[\frac{k}{m}, \frac{k+1}{m}\Big), \qquad k=0,\dots,m-1.\]

Define the coding map

\[\pi_m(x) = k \quad \text{iff } x\in I_k^{(m)}.\]

The symbolic sequence generated by the orbit of $x$ is

\[s_n^{(m)}(x) = \pi_m(T_\omega^n x) \in \{0,\dots,m-1\}.\]

This defines a symbolic dynamical system associated with m-gonic coarse-graining.

4.2 Equal-Partition Reducibility

Definition 4.1 (Equal-Partition Factor)

Let $d \mid m$. Define the block projection

\[\rho_{m\to d}(k)=\Big\lfloor \frac{k}{m/d} \Big\rfloor.\]

Then

\[\pi_d = \rho_{m\to d}\circ \pi_m.\]

In this case, the m-partition coding factors through the d-partition coding.
We say the m-partition is equal-partition reducible.

Lemma 4.2 (Composite Reducibility)

If $m$ is composite, then there exists $1<d<m$ with $d\mid m$.
Hence the m-partition is equal-partition reducible.

Proof. Immediate from Definition 4.1. ∎

Lemma 4.3 (Prime Equal-Partition Irreducibility)

If $m=p$ is prime, then there exists no nontrivial divisor $d\mid p$ with $1<d<p$.
Hence, within the class of equal partitions, the p-partition admits no nontrivial factorization.

∎

Interpretation.
Within equal-partition coarse-graining, irreducibility is guaranteed precisely by primality.

4.3 Beyond Arithmetic: Structural Absorption

Arithmetic irreducibility alone does not determine dynamical minimality.

We introduce structural absorption conditions.

Definition 4.4 (Low-Alphabet Absorption)

An m-partition coding is low-alphabet absorbable if it factors (via a finite block map) into a symbolic system over an alphabet of strictly smaller cardinality.

Formally, there exist:

an integer $k<m$,
a block radius $r$,
a map
\[\Phi: \{0,\dots,m-1\}^{2r+1} \to \{0,\dots,k-1\},\]

such that the induced sequence defines a factor shift of the original system.

This corresponds to symmetry collapse under coarse symbolic projection.

Definition 4.5 (Golden Closure Absorption)

For the golden rotation

\[\omega = \frac{\sqrt{5}-1}{2} = \frac{1}{\phi},\]

the two-interval partition generates a Sturmian sequence associated with Fibonacci substitution.

An m-partition is said to exhibit golden closure absorption if its symbolic structure factors into a Sturmian/Fibonacci regime.

4.4 Conditional Minimal Hinge

We now introduce the dynamical exclusion conditions:

(C1) Exclude low-alphabet absorption.
(C2) Exclude golden-closure absorption.
(C3) Exclude over-refinement regimes where higher-order projection dominates and coarse structure collapses into asymptotic regularity.

Theorem 4.6 (Heptagonal Minimal Hinge under Structural Exclusion)

Under conditions (C1)–(C3), the smallest equal-partition irreducible coarse-graining is

\[m = 7.\]

Proof Sketch

If $m$ is composite, reducibility follows from Lemma 4.2.
If $m$ is prime, arithmetic irreducibility holds (Lemma 4.3).
For $m=2,3$, low-alphabet absorption (C1) applies trivially.
For $m=5$, under golden rotation, the system admits Sturmian/Fibonacci factorization, hence satisfies (C2).
The next prime is $m=7$. It is arithmetically irreducible and does not fall under (C1)–(C2).
Thus 7 is the minimal structural hinge remaining.

∎

4.5 Interpretation

Seven is not selected by numerology.
It emerges as the minimal coarse-grained irreducible hinge after excluding:

trivial symmetry collapse,
golden closure stabilization,
over-projected regularization.

It is therefore the smallest polygonal regime sustaining non-absorbed rotational redistribution.

In the language of this paper:

Seven is the minimal coarse-grained irreducible hinge of toroponic redistribution.

V. Higher Modes and Projection

Higher-order partitions $m\ge 8$ generate extended dynamical possibilities. Yet within observable regimes, such modes do not persist directly.

They require projection.

Projection condenses higher-order dynamics into lower-order trace configurations. What exceeds stable representation appears only as residual pattern.

Higher modes are not eliminated.
They are translated.

Seven does not limit motion.
It marks the minimal hinge at which non-reducible persistence becomes observable.

VI. lαg and the Tropotic Axis

lαg is irreversible structural non-simultaneity under conserved redistribution.

At the ontological level, it redistributes structure.
At the kinematic level, it reorients motion.
At the ecological level, it sustains coexistence through distributed instability.

These are not separate domains. They are modes of a single axis.

We call this the Tropotic lαg Axis.

It is not a fixed center.
It is the generative hinge of orientation itself.

Between φ and θα,
between sediment and motion,
stability is not rest.

It is sustained transition.

There is no foundational simultaneity.
There is only lαg redistributing, reorienting, and sustaining coexistence.

Figure 1. The Golden Domain and the Heptagonal Hinge.
Golden-Domain_and_Heptagonal-Hinge

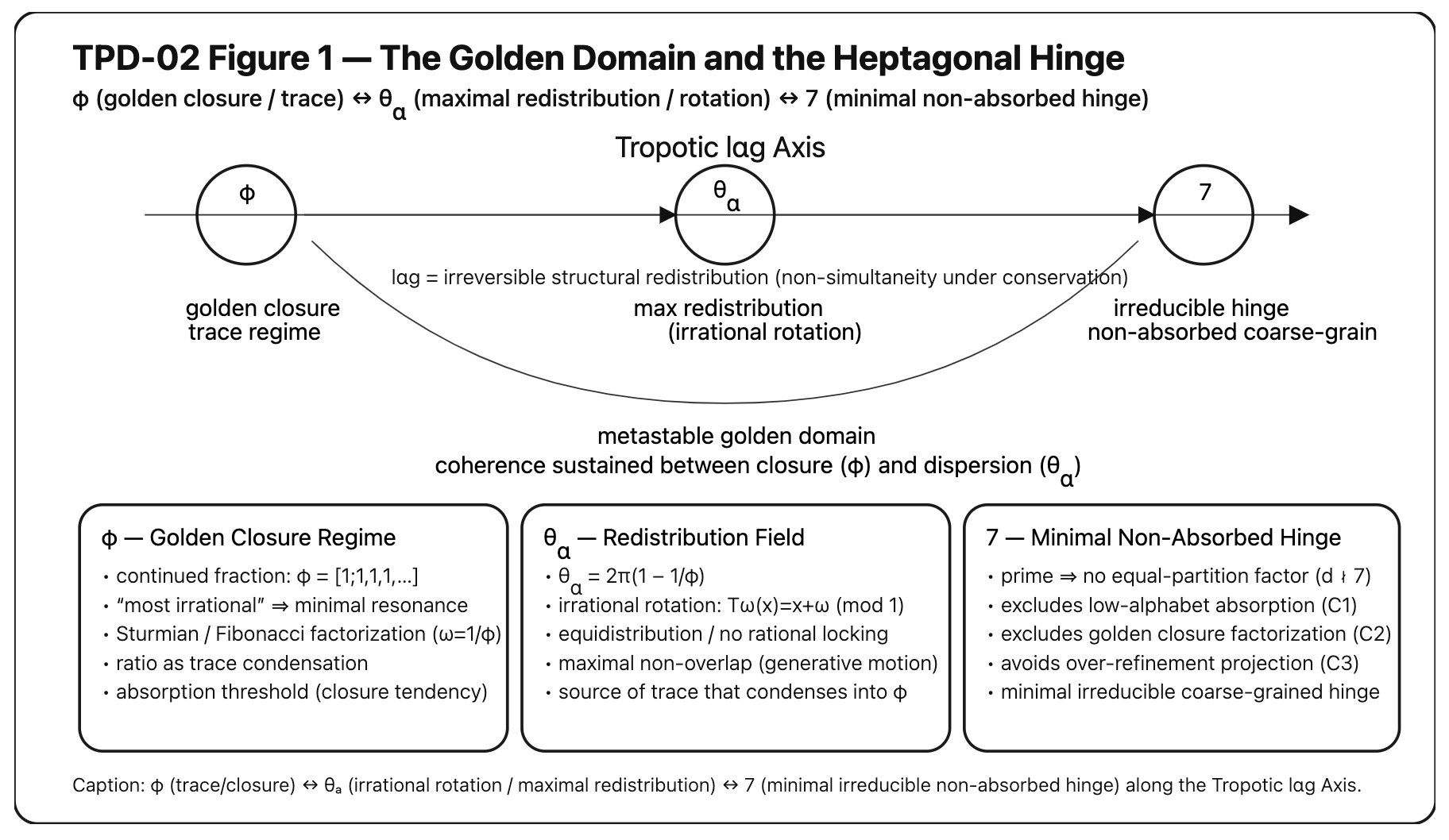
Figure 1. Structural axis of toroponic redistribution between the Golden Ratio (φ; closure/trace regime), the Golden Angle (θₐ; maximal non-simultaneity under irrational rotation), and the minimal non-absorbed coarse-grained hinge (7). The heptagonal regime is the smallest prime partition surviving equal-partition factorization and structural absorption (C1–C3), thereby sustaining coherence between closure and dispersion under lαg.

EgQE — Echo-Genesis Qualia Engine
camp-us.net

HEG-SN｜七だけが屈しない──不屈の動態学｜Toward a Minimal Structural Condition of Irreversibility

© 2025 K.E. Itekki
K.E. Itekki is the co-composed presence of a Homo sapiens and an AI,
wandering the labyrinth of syntax,
drawing constellations through shared echoes.

📬 Reach us at: contact.k.e.itekki@gmail.com

| Drafted Feb 18, 2026 · Web Feb 19, 2026 |