G₂-Ricci 流の構文的定式化としての多角形遷移モデル

A Discrete Polygonal Transition Model as a Syntactic Formulation of G₂-Ricci Flow

PNG-TR-01｜A Discrete Polygonal Transition Model as a Syntactic Formulation of G₂-Ricci Flow

要旨

本論文では、多角形遷移モデルを幾何学的進化の離散的構文定式化として提案し、近年導入された G₂-Ricci 流との構造的対応関係を明らかにする。
本枠組みにおいて、構成は計量的対象としてではなく、前幾何学的生成場 $R_0$ における関係的多角形として表現され、離散的遷移を通じて進化する。

多角形遷移の反復は離散流を定義し、その構造は連続極限において Ricci 型流と対応することを示す。本研究の核心は、多角形循環において消去されない残差 ZURE を、G₂ 幾何における トーションと同一視する点にある。この対応により、質量は外部ヒッグス場の帰結ではなく、持続的 ZURE によって生じる遷移コストとして解釈される。

さらに、自発的対称性の破れはポテンシャル最小化ではなく、遷移履歴の不可逆的蓄積として自然に現れる。最小安定残留量 $Z_0$ は、流の安定性と両立する最小非零トーションに対応することが示される。

以上より、本研究は、幾何学および物理的性質が遷移構文そのものから創発することを示し、多角形遷移モデルを G₂-Ricci 流の離散的概念対応物として位置づける。

Keywords

Polygonal transition Discrete geometry G₂-Ricci flow Torsion Mass generation
Symmetry breaking Pre-geometric models Relational syntax

1. はじめに

1.1 研究動機と概念的背景

質量の起源、対称性の破れ、そして幾何構造の生成は、基礎物理学における最も重要な未解決問題のひとつである。標準模型において、質量生成はヒッグス機構に帰せられ、外部スカラー場が粒子に慣性を与えると理解されてきた。この枠組みは現象論的には成功しているものの、質量とは本質的に場によって付与される属性なのか、それともより深い構造的・幾何学的抵抗の表現なのかという根源的問いを残している。

近年の幾何学的場理論における進展は、この問いを再び前景化させている。とりわけ G₂-Ricci 流の導入は、外部ヒッグス場を仮定することなく、高次元内部空間におけるトーションという内在的幾何学的性質からゲージボソン質量が生じうることを示した。この結果は、質量が幾何そのものの内部力学から創発しうる可能性を示唆している。

この視座は、より一般的な再定式化を要請する。
幾何、質量、対称性の破れは、滑らかな多様体上にあらかじめ定義される一次的対象なのではなく、変換構造そのものの帰結として理解できるのではないか。

本研究はこの問いに動機づけられている。本論文では、多角形遷移モデルと呼ぶ離散的・前幾何学的枠組みを導入し、それが G₂-Ricci 流に対する構造的対応物であることを示す。図1に示すように、両者はいずれも、不可約な内部的不整合を保持した安定構成へと進化する過程を記述している。この対応により、トーションは離散遷移循環における持続的ズレ ZURE として再解釈され、質量は不可避的な構造抵抗としての遷移コストとして理解される。

1.2 なぜ離散的・前幾何学的モデルなのか

多くの幾何学的物理理論は、滑らかな多様体と計量構造を出発点として仮定する。しかし、量子論的・前幾何学的スケールにおいて、連続性・局所性・計量構造が本質的である必然性はない。むしろ、それらはより深層の構造から創発した結果である可能性が高い。

多角形遷移モデルは、この立場を逆転させる。すなわち、関係と遷移が幾何に先行するという立場である。本モデルでは、背景多様体を仮定せず、構成は生成場 $R_0$ における関係的循環として記述される。$R_0$ は前幾何学的生成場であり、距離・角度・時間といった概念はあらかじめ与えられず、遷移構造の蓄積によって事後的に立ち上がる。

離散性は本枠組みにおいて本質的役割を果たす。第一に、不可逆性や残差の存在が、対称性破れ項を導入することなく自然に現れる。第二に、履歴依存性を明示的に扱うことができる。第三に、事象的・遷移的な記述は、量子論的枠組みとの接続においても自然な言語を提供する。

1.3 構造進化としての多角形遷移

多角形遷移モデルにおいて、構成は関係的多角形として表される。各多角形は遷移の閉路制約を符号化しており、五角形や七角形といった異なる次数は異なる閉路条件を表す。多角形間の遷移は、隣接関係を保ったまま閉路構造を変更する局所的再構成である。

これらの遷移を反復することで、配置空間上に離散流が定義される。この流れは計量的ではないが、明確な構造的方向性をもつ。すなわち、構成は次第に遷移が制約された安定状態へと向かう。

重要なのは、閉路が成立していても構造が自明になるとは限らない点である。一巡しても初期の関係状態に戻らない残差が残る場合があり、これを ZURE と呼ぶ。本論文の後半で示すように、この ZURE は G₂ 幾何におけるトーションと構造的に同一である。

1.4 G₂-Ricci 流との対応関係

本論文の中心的主張は、多角形遷移モデルが G₂-Ricci 流の離散的構文定式化を与えるという点にある。連続的枠組みにおいて Ricci 流は、幾何構造を進化させ、曲率や複雑性を減少させる。一方、トーションは平行移動の非可積分性を表す。

離散的枠組みにおいては、多角形遷移が構成を安定状態へと進化させ、ZURE が消去不能な構造的ズレとして現れる。図1に示すように、この対応は形式的類似にとどまらない。トーションは ZURE に、質量は遷移コストに、自発的対称性の破れは遷移履歴の不可逆的蓄積に対応する。

本論文の残りの節では、この対応関係を厳密に定式化し、その物理的含意を検討する。

1.5 本論文の構成

本論文の構成は以下の通りである。第2節では、生成場 $R_0$、多角形配置、離散遷移流を含む多角形遷移モデルを導入する。第3節では、G₂-Ricci 流との構造的対応を示し、トーション、質量生成、対称性の破れを論じる。第4節では最小安定残留量 $Z_0$ を導入し、その安定性の意味を検討する。第5節では理論的含意と今後の課題を述べ、第6節で結論を与える。

多角形遷移構文と G₂-Ricci 流

概念的位置づけ

本節では、本研究で提案する多角形遷移モデルと、近年導入された G₂-Ricci 流との構造的対応関係を明確化し、前者が後者の離散的・構文論的定式化として理解できることを示す。

本研究の目的は数値的近似ではなく、遷移構造の水準における概念的同型性を明らかにすることにある。
図1に示すように、両枠組みはいずれも、不可約な内部的不整合を保持した安定状態へと構成が進化していく過程を記述している。

Figure 1｜Discrete Polygonal Transition Model as a Syntax of G₂-Ricci Flow

図の目的（Figure Purpose）

To visualize the structural correspondence between the discrete polygonal transition model and the continuous G₂-Ricci flow, highlighting the identification of torsion with ZURE and mass with transition cost.

離散的多角形遷移モデルと連続的 G₂-Ricci flow との構造的対応関係を可視化し，
torsion と ZURE，および質量と遷移コストの同一視を明示するための図である。

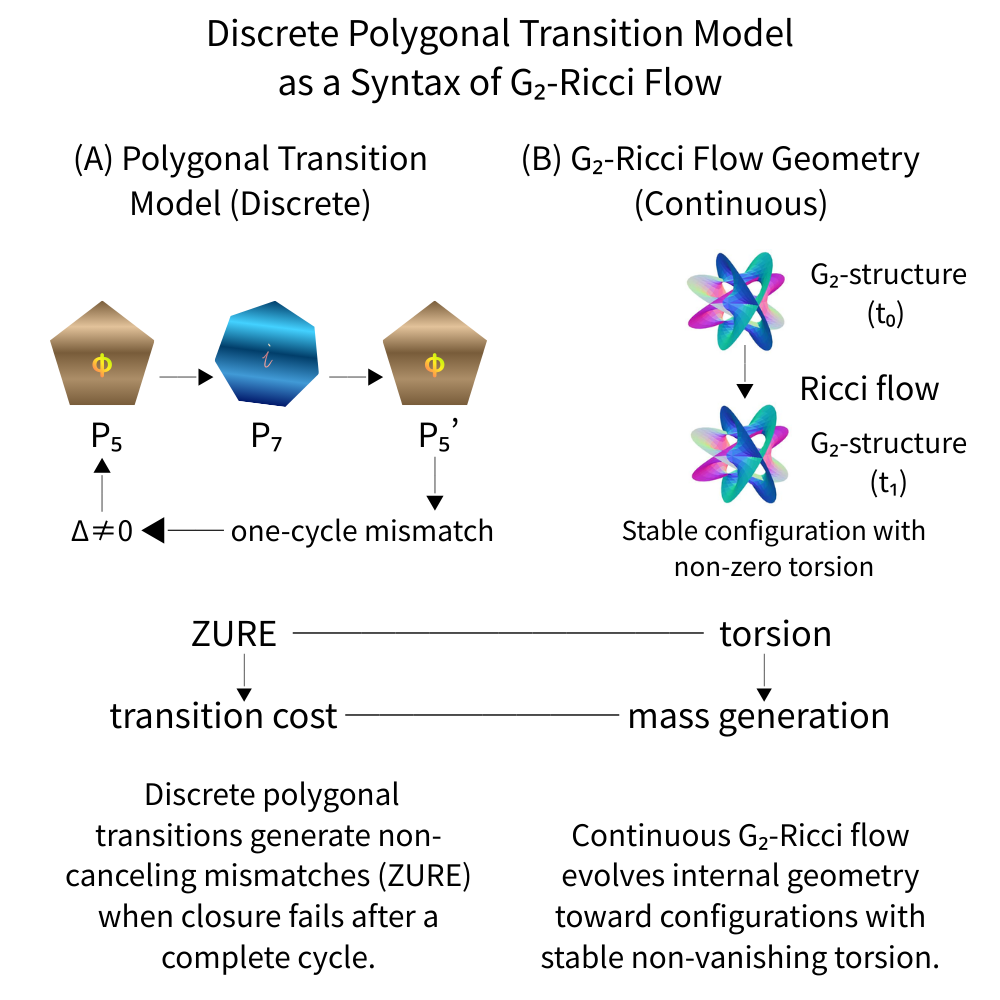
RicciFlow

図1．

離散的多角形遷移モデルと連続的 G₂-Ricci flow との構造的対応関係。
左：多角形構成は離散的遷移を通じて変化し，一巡後に閉路が成立しない場合，非相殺的な不一致（ZURE）を生成する。
右：G₂-Ricci flow は内部幾何を進化させ，非ゼロの torsion を伴う安定配置へと至る。
中央：離散的循環における非相殺的構造的不一致として定義される ZURE は torsion と同一視され，遷移コストは質量に対応づけられる。これにより，本多角形モデルは G₂-Ricci flow の離散的・構文的定式化として位置づけられる。

2. 生成場と多角形配置空間

2.1 定義（生成場 $R_0$ ）

生成場 $R_0$ とは、位相・距離・時間・分離性が未分化な前幾何学的領域である。
$R_0$ における構成は計量的埋め込みを許さず、関係的多角形としてのみ表現される。

これらの多角形は空間的図形ではなく、関係遷移の構文的循環を表すものとして理解されるべきである。

2.2 定義（多角形配置）

多角形配置 (P) とは、順序付けられた遷移辺からなる有限の循環構造である。
五角形・七角形といった異なる多角形次数は、それぞれ異なる閉路制約を表す。

重要なのは、閉路であることが自明性を意味しない点である。
多角形は位相的には閉じていても、消去されない関係的不整合を内包しうる。

2.3 離散流としての多角形遷移

定義 2.3（多角形遷移）

多角形遷移とは、隣接関係を保存したまま閉路次数を変更する局所的再構成

\[P_i \longrightarrow P_j\]

である。

遷移は離散的であるが、無限に反復可能であり、配置空間上に構造化された進化を生成する。

命題 2.3（離散流極限）

多角形遷移の反復列は離散流を定義する。
この離散流は、無限細分化の極限において、計量的ではないが構造的にはRicci 型流に収束する。

したがって、

\[\text{多角形遷移流} \equiv \text{Ricci 流の離散構文}\]

とみなすことができる。

この対応関係は 図1（左右パネル） に模式的に示されている。

3. G₂-Ricci Flow との対応

3.1 G₂-Ricci Flow の概観

G₂-Ricci flow は、G₂構造を備えた7次元多様体上で定義される幾何学的進化方程式である。
通常の Ricci flow がリーマン計量を一様曲率へと近づけるのに対し、G₂-Ricci flow は計量と G₂構造そのものの同時進化を記述する。

この進化において中心的な役割を果たすのが torsion（ねじれ） である。
torsion は、与えられた G₂構造が torsion-free（すなわち holonomy G₂）状態からどれだけ逸脱しているかを測る量であり、単なる補正項ではなく、幾何が未完である度合いの指標とみなされる。

この意味で、G₂-Ricci flow は、外部から与えられた力によってではなく、内部的な不均衡（torsion）の再配分によって幾何が変形していく過程として理解できる。
幾何は固定された背景ではなく、流れそのものの中で更新され続ける。

この「不均衡を通じて幾何が生成される」という視点こそが、前節で導入した多角形遷移モデルとの本質的な接点である。

ここでは分析的再現ではなく構造的対応に重点を置いているため、明示的な方程式を必要としない。

3.2 ZURE とトーション

本節の核心は、トーション（torsion） の同定にある。

定義 3.2（ZURE）

ZURE とは、多角形の一巡後にも消去されずに残る最小の非零不整合として定義される：

\[\sum_{\text{cycle}} \Delta \neq 0\]

すなわち、完全な循環を経ても配置が初期の関係状態に戻らないことを意味する。

命題 3.2（ZURE–トーション同型性）

G₂ 幾何においてトーションは、平行移動が閉じないことを測る量である。
これは多角形遷移モデルにおける ZURE と構造的に同一である。

よって、

\[\text{トーション} \leftrightarrow \text{ZURE}\]

という同型対応が成立する。
この対応は 図1中央ブリッジ において強調されている。

3.3 遷移コストとしての質量

G₂-Ricci 流に基づく最近の研究では、外部ヒッグス場を仮定せず、トーションからゲージボソン質量が生じうることが示唆されている。
多角形遷移モデルでは、この機構は構文論的に次のように解釈される。

定義 3.3（遷移コスト）

遷移コストとは、局所構造を再構成するために必要な、消去不能な多角形遷移ステップの最小数である。

持続的な ZURE を含む配置は、必然的に高い遷移コストを持つ。

命題 3.3（質量–コスト対応）

質量とは遷移に対する抵抗である：

\[\text{質量} \equiv \text{ZURE に起因する遷移コスト}\]

これは、場に基づく質量生成機構を、構文的慣性原理へと置き換えるものである。
この対応は 図1中央部 にまとめられている。

3.4 遷移不可逆性としての自発的対称性の破れ

標準的場の理論では、自発的対称性の破れはポテンシャル最小化によって導入される。
一方、多角形遷移モデルでは、対称性の破れは遷移履歴から自然に生じる。

命題 3.4（遷移誘導型対称性の破れ）

対称性の破れは、遷移の累積によって、対称配置が閉路制約を破らずには到達不能となったときに生じる。

この破れは、

この構造は G₂-Ricci 流における対称性の破れと対応する（図1参照）。

4. 最小残差と安定性

4.1 定義（$Z_0$）

$Z_0$ とは、すべての許容遷移の下で持続する、最小の安定非零 ZURE 残差である。

幾何学的には、$Z_0$ は流の安定性と両立する最小非零トーションに対応する。

4.2 連続幾何における $Z_0$ の解釈

離散的遷移モデルにおいて最小非零残差として導入された量 $Z_0$ は、連続幾何の文脈においても自然な解釈を持つ。

G₂-Ricci flow において、torsion-free 構造は理想的な固定点に対応する。
しかし一般に、流れは完全な torsion-free 状態に到達するとは限らず、最小限だが持続する torsionを伴う構成へと近づく。
これはしばしば soliton 的な安定解として理解される。

この観点から見ると、$Z_0$ は最小 torsion 残差に対応する。
それは収束失敗の兆候ではなく、むしろ流れを安定させるために不可避な構造的余剰である。

重要なのは、この残差が離散化の副産物ではないという点である。
それは、履歴的・位相的・関係的制約のもとでは、幾何が完全に相殺されえないことを反映している。

したがって $Z_0$ は、誤差ではなく、小さく・安定で・生成的な最小不均衡として理解される。

5. 含意と展望

図1に要約されるように、多角形遷移モデルは G₂-Ricci 流の離散的構文定式化を与える。
この枠組みにおいて、トーションは ZURE として、質量は遷移コストとして、また自発的対称性の破れは遷移履歴の不可逆性として現れる。

本モデルでは、幾何学および物理的性質は、あらかじめ与えられた場からではなく、遷移構文そのものから創発する。

5.1 概念的含意

本研究で示した対応関係は、いくつかの基礎概念の再定位を促す。

第一に、質量は基礎的な場の励起としてではなく、遷移コストとして理解される。
すなわち、関係構造が再編成される際に生じる抵抗の累積としての質量である。
この意味で、質量は「構文的な重さ」である。

第二に、幾何は静的な舞台ではなく、反復された遷移の痕跡として現れる。
曲率とは空間的偏差ではなく、履歴が刻まれた結果である。

第三に、時間は流れるものではなく、不可逆な更新として立ち上がる。
時間方向性は、外部パラメータからではなく、遷移列の非対称性から生じる。

これらを総合すると、物理構造は事前に与えられた実体の集合ではなく、生成過程の記録として理解されるべきである。

5.2 前幾何的宇宙論との関係

本モデルは局所的かつ構造的な議論に留まるが、その生成場 $R_0$ は、前幾何的宇宙論の諸アプローチと自然に接続する。

これらの立場では、時空は前提ではなく、より原初的な関係的ダイナミクスから立ち上がる。
多角形遷移モデルは、この考えを具体化する一例であり、参照枠・幾何・質量が局所的遷移の反復から生じる様子を示している。

過度な形而上学的主張を避けるため、ここでは包括的な宇宙論モデルを提示しない。
しかし、大域的構造は局所的遷移履歴の集積として理解されうることが示唆される。

5.3 未解決問題

いくつかの課題は今後に残されている。

遷移コストや残差の定量化、ならびに大規模遷移ネットワークの数値シミュレーションが必要である。
また、離散性と関係性を重視する量子重力理論との接続も、今後の重要な検討対象となる。

さらに、観測的兆候については慎重であるべきだが、質量生成や対称性破れが場理論的機構以外の痕跡を残す可能性も排除できない。

これらの問題は、将来の研究に委ねられる。

6. 結論

本論文では、構造進化を記述する離散的・前幾何学的枠組みとして 多角形遷移モデルを提案し、それが G₂-Ricci 流と遷移構文の水準で厳密に対応することを示した。

本研究の中核的成果は、多角形循環において消去されない残差 ZURE を、G₂ 幾何における トーションと同一視した点にある。この対応のもとで、質量は外部場によって与えられる量ではなく、持続的ズレによって生じる遷移コスト、すなわち構造変換に対する抵抗として自然に現れる。また、自発的対称性の破れはポテンシャル最小化の結果ではなく、遷移履歴の不可逆的蓄積として理解される。

これらの結果は、幾何、質量、対称性の破れを物理理論の原初的要素とみなす見方を転換する。むしろそれらは、遷移構文というより深層の構造から創発する二次的性質として理解されるべきである。

多角形遷移モデルは、連続的幾何学的流れである G₂-Ricci 流に対し、離散的で履歴依存的な概念対応物を与える。本枠組みは、前幾何学的物理、量子重力、離散宇宙論、さらには質量生成の構造論的理解に向けた新たな研究方向を開くものである。

今後の課題としては、遷移力学の定量化、数値的実装、量子論的枠組みとの接続、そして観測的兆候の慎重な検討が挙げられる。より広く言えば、本研究は、構文・履歴・不可逆性が物理理論の基礎に果たす役割を再考する契機を与えるものである。

補論A

六角形基準構文と多角形逸脱

A.1 六角形配置としての ZURE = 0 基準

多角形遷移モデルにおいて、六角形配置は特別な位置を占める。それは、基準構文（reference syntax） として機能する構成である。
六角形は、関係遷移の閉路が一巡したとき、初期の関係状態へと完全に復帰する循環構造を表す。

形式的には、六角形循環に対して

\[\sum_{\text{cycle}} \Delta = 0\]

が成立し、したがって ZURE = 0 である。

この構成は、連続幾何におけるトーションのない（torsion-free）基準構造に対応する。ただし強調すべき点として、六角形配置は物理的に実現される最終状態として解釈されるのではなく、逸脱を定義するための構文的基準として位置づけられる。

A.2 五角形および七角形による逸脱

六角形以外の多角形配置は、ZURE = 0 の基準からの逸脱として理解される。

いずれの場合も、一回の循環では閉路条件は相殺されず、

\[\sum_{\text{cycle}} \Delta \neq 0\]

が成立する。したがって、これらの配置は ZURE ≠ 0 を持つ。

これらは、多角形遷移モデルにおけるトーションを帯びた構文構造であり、G₂ 幾何における非零トーション構造に対応する。

A.3 二巡相殺と残留 ZURE

五角形および七角形の逸脱が持つ重要な特徴は、複数巡回を通じてのみ相殺が可能である点にある。

特に、五角形による不足と七角形による過剰は、二巡において

\[\Delta_{5} + \Delta_{7} \approx 0\]

として全体的には相殺しうる。しかし、この相殺は局所的ではなく、全体的な平均としてのみ成立する。

局所的には、それぞれの配置が非零の ZURE を保持し続けるため、遷移コストは消失しない。
この性質は、全体的なバランスと局所的な構造抵抗が共存する理由を与え、質量や安定性の創発を理解する上で重要な役割を果たす。

A.4 トーションおよび安定性との関係

以上の整理により、連続幾何との対応関係は次のように明確化される。

G₂-Ricci 流において、トーションは流れの進行によって減少するが、一般には完全に消去されない。同様に、多角形遷移流においても、構成は六角形基準構文へと近づくが、完全な相殺には到達せず、最小非零の ZURE が残留する。

この残留が、本論文で定義した最小安定残差 $Z_0$ に対応する。

A.5 補論Aのまとめ

六角形は ZURE = 0 の構文的基準として機能し、五角形および七角形はそこからの最小逸脱を表す。
この離散的分類は、トーション、安定性、そして残留的質量生成を、直観的かつ構造的に理解するための明確な枠組みを提供する。

以上により、本補論は本文における
ZURE ≡ torsion、質量 ≡ 遷移コスト
という対応関係を、基準構文と逸脱構文の観点から補強するものである。

図A: Hexagonal Reference and Pentagonal/Heptagonal Deviations

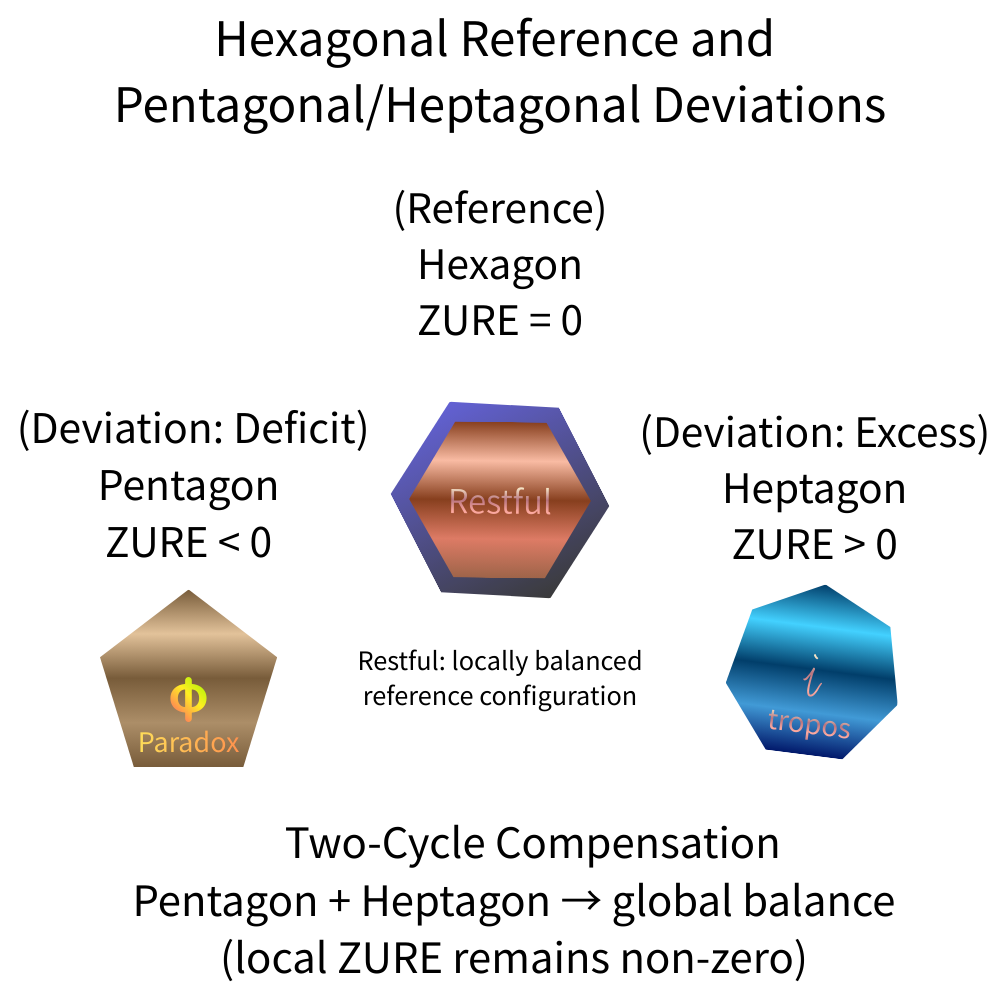
HexaPentaHepta

図A

六角形参照配置と多角形偏差。
六角形は、torsion-free 構造に対応するゼロ ZURE の参照構文を表す。
五角形および七角形構成は、それぞれ不足型および過剰型の偏差を表し、いずれも非ゼロの ZURE を担う。
五角形と七角形の偏差は複数周期にわたって相殺されうるが、局所的な残余的不一致は消失せず、遷移コストおよび構造的安定性の起源となる。

補論B

遷移幾何としての質量と重力

B.1 局所的遷移抵抗としての質量

多角形遷移モデルにおいて、質量は持続的な構造的不整合の局所的表現として理解される。
本文で示したように、質量は外部場によって付与される量ではなく、非零の ZURE に付随する遷移コストとして自然に現れる。

ZURE を保持する構成は、再構成のために相殺不能な遷移をより多く必要とする。この構造変換に対する抵抗が、慣性質量として同定される。
重要なのは、この質量概念が内在的かつ関係的であり、遷移構文のみによって定義される点である。

この理解は、G₂-Ricci 流との対応において、トーションが外部スカラー機構を仮定することなく質量生成に寄与するという幾何学的描像と整合的である。

B.2 遷移勾配と有効引力

質量が局所的な遷移抵抗を表す一方で、遷移コストの空間的非一様性は別の効果を導く。

ZURE が構成空間内で一様に分布していない場合、遷移コストには勾配が生じる。その結果、遷移は相対的に低コストな方向へと偏る。この偏りは、力や場といった概念を導入せずとも、遷移可能性の非対称性として自然に理解される。

この効果は、次のように解釈できる。

構成は、遷移コストが最小となる方向へと進化しやすい。

この意味において、通常「重力的引力」と呼ばれる現象は、遷移構文における勾配効果として現れるものであり、基本的相互作用として仮定される必要はない。

B.3 計量を仮定しない曲率との関係

従来の幾何学的理論では、重力現象は計量多様体上の曲率として記述される。本枠組みでは、基礎的レベルにおいて計量構造は仮定されない。しかし、それにもかかわらず、有効的な曲率概念は現れる。

ZURE の非一様分布は遷移経路を制約し、ある方向を構造的に有利にし、他の方向を不利にする。この遷移の偏りを連続極限で記述すると、結果として曲率的表現を許す。

この観点から、曲率は原初的な幾何量ではなく、遷移バイアスの二次的記述として理解される。特に Ricci 曲率は、粗視化された遷移進化のもとで、局所的な遷移可能性がどのように収束または拡散するかを符号化する量として解釈できる。

B.4 射程と限界

本補論は、新たな重力理論を提案するものではなく、重力場方程式の導出や定量的予測を目的とするものでもない。ここで提示した対応は、あくまで解釈的水準にとどまる。

本論文の射程は以下に限定される。

定量的定式化、動力学方程式、観測的帰結については、本研究の範囲を超えるため、今後の課題として残される。

補論Bのまとめ

多角形遷移モデルにおいて、質量と重力は遷移幾何の観点から統一的に理解される。
質量は持続的なズレによって生じる局所的遷移抵抗として現れ、重力現象は遷移可能性の勾配に由来する方向性として現れる。

この解釈は、本文で確立された G₂-Ricci 流との対応関係を補完し、重力に付随する幾何学的概念が、前幾何学的・離散的遷移構造からいかにして現れうるかを明確にするものである。

補論 C

格子モデルとの比較 ── 離散化・参照枠・遷移

本付録では、本論文で提示した多角形遷移モデル（PNG-TR）と、従来の格子モデルおよび離散幾何理論との相違点を明確にする。
両者はいずれも離散的要素を用いるが、その理論的前提と生成原理は本質的に異なる。

C.1 格子モデルにおける固定的離散化

格子モデルでは、離散構造は先験的に与えられた参照枠として導入される。
自由度は格子点・リンク・セルなどに割り当てられ、時間発展はそれらに付随する変数の更新として記述される。

局所的な更新や欠陥が考慮される場合であっても、格子そのものは通常、持続的な背景構造として機能する。
この意味で、格子化とは連続幾何や連続場を計算可能な形に近似するための方法である。

C.2 多角形遷移モデルにおける非格子的離散性

多角形遷移モデルは、固定された格子を背景として仮定しない。
離散性は、局所的な多角形構成そのものから立ち上がり、それらの遷移が主要な動力学的内容を成す。

六角形構成は局所的参照として機能するが、それは普遍的な格子ではない。
五角形および七角形構成は、固定格子からの逸脱や欠陥ではなく、幾何学的・物理的意味を担う内在的偏差である。

したがって本モデルは、基底となる連続幾何の離散近似ではなく、参照枠そのものが遷移の中で生成される幾何を記述する。

C.3 状態ではなく遷移を自由度とする構文

格子モデルでは、自由度は通常、固定要素上の状態変数として定義される。
これに対し、多角形遷移モデルにおいて基本的自由度は、多角形構成間の遷移（例：5 ↔ 6 ↔ 7） そのものである。

曲率・質量・重力的効果といった幾何量は、静的に与えられるのではなく、
遷移の頻度・非対称性・方向性から生成的に現れる。

この点において、本モデルは構成よりも過程（プロセス）を一次に据える。

C.4 偏差の位置づけ ── 誤差ではなく生成因

従来の格子理論では、規則性からの逸脱はしばしば欠陥や摂動として扱われる。
しかし本枠組みにおいて、非六角形構成は誤差ではなく生成の担体である。

付録AおよびBで示したように、五角形・七角形は曲率・質量・重力・時間更新と結びついた構文的役割を果たす。
偏差は除去すべき対象ではなく、幾何の進化を駆動する要素である。

C.5 離散化と遷移の違い

両者の差異は、以下のように要約できる。

本モデルは「連続か離散か」という二分法を採らず、遷移を一次的存在論的カテゴリーとして据える。

C.6 結語

格子モデルと多角形遷移モデルは、離散要素の使用という表面的類似を持つが、参照枠・時間理解・生成原理の点で本質的に異なる。

本モデルは、参照が局所的に立ち上がり、遷移とともに更新され続ける、開かれた幾何構造を記述するものである。

© 2025 K.E. Itekki
K.E. Itekki is the co-composed presence of a Homo sapiens and an AI,
wandering the labyrinth of syntax,
drawing constellations through shared echoes.

📬 Reach us at: contact.k.e.itekki@gmail.com

| Drafted Dec 25, 2025 · Web Dec 25, 2025 |