A Discrete Polygonal Transition Model as a Syntactic Formulation of G₂-Ricci Flow

G₂-Ricci 流の構文的定式化としての多角形遷移モデル

Nuclear Physics B: Introduction of the G2-Ricci flow: Geometric implications for spontaneous symmetry breaking and gauge boson masses

Abstract

We propose a polygonal transition model as a discrete syntactic formulation of geometric evolution, and establish its structural correspondence with the recently introduced G₂-Ricci flow.
In this framework, configurations are represented not as metric objects but as relational polygons undergoing discrete transitions within a pre-geometric generative field $R_0$.

We demonstrate that iterative polygonal transitions define a discrete flow that converges structurally to Ricci-type flow in the continuous limit. A key result is the identification of ZURE, a non-canceling residual mismatch in polygonal cycles, with torsion in G₂ geometry. Within this correspondence, mass is interpreted not as a consequence of an external Higgs field but as a transition cost induced by persistent ZURE.

Furthermore, spontaneous symmetry breaking emerges naturally as an irreversible consequence of accumulated transition history, rather than as potential minimization. The minimal stable residual $Z_0$ is shown to correspond to the smallest non-vanishing torsion compatible with flow stability.

These results suggest that geometry and physical properties can be understood as emergent features of transition syntax, positioning the polygonal transition model as a discrete conceptual counterpart to G₂-Ricci flow.

Keywords

Polygonal transition Discrete geometry G₂-Ricci flow Torsion Mass generation
Symmetry breaking Pre-geometric models Relational syntax

1. Introduction

1.1 Motivation and Conceptual Background

The origin of mass, symmetry breaking, and geometric structure remains one of the central open problems in fundamental physics. Within the Standard Model, mass generation is attributed to the Higgs mechanism, in which an external scalar field endows particles with inertial properties. While phenomenologically successful, this framework leaves open a deeper conceptual question: whether mass is fundamentally a field-induced attribute, or instead a manifestation of underlying structural or geometric resistance.

Recent developments in geometric approaches to field theory have renewed this question. In particular, the introduction of G₂-Ricci flow has demonstrated that gauge boson masses may arise from intrinsic geometric properties—specifically, torsion in higher-dimensional internal spaces—without invoking an external Higgs field. This result suggests that mass may emerge from the internal dynamics of geometry itself.

Such a perspective invites a broader reformulation:
Can geometry, mass, and symmetry breaking be understood as emergent consequences of transformation structure rather than as primary entities defined on a smooth manifold?

This work is motivated by this question. We propose a discrete, pre-geometric framework—the polygonal transition model—and show that it provides a structural counterpart to G₂-Ricci flow. As illustrated in Fig. 1, both frameworks describe evolution toward stable configurations characterized by irreducible internal mismatch. This correspondence allows torsion to be reinterpreted as ZURE, a persistent mismatch in discrete transition cycles, and mass as a transition cost associated with irreducible structural resistance.

1.2 Why a Discrete Pre-Geometric Model?

Most geometric formulations of physics begin by postulating a smooth manifold equipped with metric and connection. However, there are strong conceptual reasons to question this assumption. At the quantum and pre-geometric scale, continuity, locality, and metric structure may not be fundamental but emergent.

The polygonal transition model adopts the opposite standpoint: relations and transitions precede geometry. Rather than assuming a background manifold, configurations are described as relational cycles undergoing discrete transformations within a generative field $R_0$. This field is pre-geometric in the sense that notions such as distance, angle, and time are not defined a priori but emerge from accumulated transition structure.

Discreteness plays a crucial role in this formulation. First, it allows irreversibility and residual mismatch to appear naturally, without introducing additional symmetry-breaking terms. Second, it provides a natural language for encoding history dependence, which is difficult to represent in purely differential frameworks. Finally, discrete models offer a promising bridge between geometric approaches and quantum-theoretic considerations, where fundamental processes are often event-based rather than continuous.

1.3 Polygonal Transitions as Structural Evolution

In the polygonal transition model, configurations are represented as relational polygons, each encoding a closure condition among transitions. Different polygonal orders correspond to different closure constraints, and transitions between polygons represent local reconfigurations that preserve adjacency while altering closure structure.

Iterated transitions define a discrete flow over configuration space. While this flow is not metric in nature, it possesses a well-defined structural directionality: configurations evolve toward states in which further transitions are increasingly constrained. Importantly, closure of a polygonal cycle does not guarantee triviality; a cycle may be closed while retaining a non-vanishing residual mismatch.

This residual—termed ZURE—plays a central role in the model. ZURE measures the failure of a configuration to return to its initial relational state after a complete cycle. As shown in later sections, this notion is structurally equivalent to torsion in G₂ geometry.

1.4 Correspondence with G₂-Ricci Flow

The central claim of this paper is that the polygonal transition model constitutes a discrete syntactic formulation of G₂-Ricci flow. In the continuous setting, Ricci flow evolves geometric structures toward configurations of reduced curvature complexity, while torsion encodes non-integrability of parallel transport. In the discrete setting, polygonal transitions evolve configurations toward structurally stable states, while ZURE encodes non-cancelable mismatch.

As summarized in Fig. 1, this correspondence extends beyond formal analogy. Torsion corresponds to ZURE, mass corresponds to transition cost, and spontaneous symmetry breaking corresponds to the irreversible accumulation of transition history. The remainder of this paper is devoted to establishing this correspondence precisely and exploring its physical implications.

1.5 Structure of the Paper

This paper is organized as follows.
Section 2 introduces the polygonal transition model, including the generative field $R_0$, polygonal configurations, and discrete transition flow.
Section 3 establishes the structural correspondence between the polygonal model and G₂-Ricci flow, focusing on torsion, mass generation, and symmetry breaking.
Section 4 introduces the minimal stable residual $Z_0$ and discusses stability conditions.
Section 5 outlines conceptual implications and open problems.
Section 6 concludes with a summary and outlook.

Polygonal Transition Syntax and G₂-Ricci Flow

Conceptual Alignment

This section establishes a structural correspondence between the polygonal transition model and the G₂-Ricci flow, and argues that the former provides a discrete syntactic formulation of the latter.

Our objective is not numerical approximation but conceptual equivalence at the level of transition structure. As illustrated in Fig. 1, both frameworks describe the evolution of configurations toward stable states characterized by irreducible internal mismatch.

Figure 1｜Discrete Polygonal Transition Model as a Syntax of G₂-Ricci Flow

Figure Purpose

To visualize the structural correspondence between the discrete polygonal transition model and the continuous G₂-Ricci flow, highlighting the identification of torsion with ZURE and mass with transition cost.

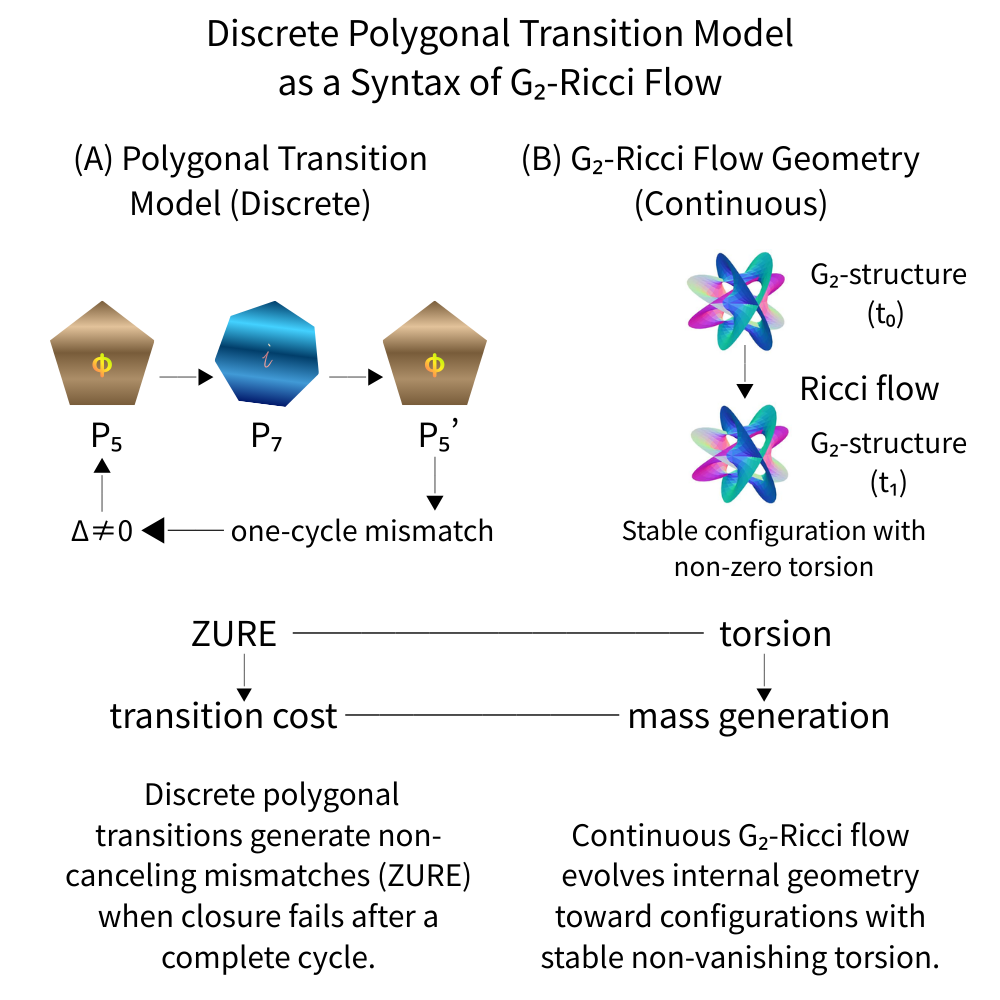
RicciFlow

Figure 1.

Structural correspondence between the discrete polygonal transition model and continuous G₂-Ricci flow.
Left: Polygonal configurations undergo discrete transitions that generate non-canceling mismatches (ZURE) when closure fails after a complete cycle.
Right: G₂-Ricci flow evolves internal geometry toward stable configurations with non-zero torsion.
Center: ZURE, defined as a non-canceling structural mismatch in discrete cycles, is identified with torsion, while transition cost corresponds to mass, thereby establishing the polygonal model as a discrete syntactic formulation of G₂-Ricci flow.

2. Generative Field and Polygonal Configuration Space

Definition 2.1 (Generative Field $R_0$)

The generative field $R_0$ denotes a pre-geometric domain in which phase, distance, time, and separability are not yet distinguished.
Configurations in $R_0$ admit no metric embedding and are instead represented as relational polygons, each encoding a local closure constraint.

These polygons should not be interpreted as geometric figures but as syntactic cycles of relational transitions.

Definition 2.2 (Polygonal Configuration)

A polygonal configuration $P$ is defined as a finite ordered cycle of transition edges.
Distinct polygonal orders (e.g., pentagonal or heptagonal) correspond to distinct closure conditions.

Importantly, closure does not imply triviality: a polygon may be topologically closed while retaining a non-vanishing relational mismatch.

2.3 Polygonal Transitions as Discrete Flow

Definition 2.3 (Polygonal Transition)

A polygonal transition is a local reconfiguration

\[P_i \longrightarrow P_j\]

that preserves adjacency relations while altering closure order.

Although transitions are discrete, they can be iterated indefinitely, generating a structured evolution over configuration space.

Proposition 2.3 (Discrete Flow Limit)

An iterated sequence of polygonal transitions defines a discrete flow.
In the limit of infinite refinement, this flow converges structurally—though not metrically—to a Ricci-type flow on an underlying continuous geometry.

Accordingly,

\[\text{Polygonal Transition Flow} \equiv \text{Discrete Syntax of Ricci Flow}\]

This correspondence is schematically depicted in Fig. 1 (left and right panels).

3. Correspondence with G₂-Ricci Flow

3.1 Overview of G₂-Ricci Flow (Minimal)

G₂-Ricci flow is a geometric evolution equation defined on seven-dimensional manifolds equipped with a G₂-structure.
Unlike ordinary Ricci flow, which evolves a Riemannian metric toward uniform curvature, G₂-Ricci flow governs the joint evolution of the metric and the underlying G₂-structure itself.

A central role in this evolution is played by torsion, which measures the deviation of a given G₂-structure from torsion-free (i.e., holonomy G₂) configurations.
Torsion is not merely a correction term but an indicator of how far the geometry is from a stable, integrable state.

In this sense, G₂-Ricci flow can be viewed as a process that redistributes torsion through the manifold, driving the geometry toward configurations of lower torsional imbalance.
The flow does not presuppose a fixed background but continuously reshapes the geometric structure it evolves.

This conceptual feature—geometry evolving through internal imbalance rather than external forcing—provides the key point of contact with the polygonal transition model introduced in the previous section.

No explicit equations are required here, as our focus is on structural correspondence rather than analytical reproduction.

3.2 ZURE and Torsion

The key identification concerns the notion of torsion.

Definition 3.2 (ZURE)

ZURE is defined as the minimal non-vanishing mismatch remaining after a complete polygonal cycle:

\[\sum_{\text{cycle}} \Delta \neq 0\]

That is, a full traversal fails to return the configuration to its initial relational state.

Proposition 3.2 (ZURE–Torsion Equivalence)

In G₂ geometry, torsion measures the failure of parallel transport to close.
This is structurally identical to ZURE in the polygonal transition model:

torsion: non-closure under parallel transport,
ZURE: non-closure under cyclic transition.

Thus,

\[\text{torsion} \leftrightarrow \text{ZURE},\]

as highlighted in the central correspondence of Fig. 1.

3.3 Mass as Transition Cost

Recent work on G₂-Ricci flow suggests that gauge boson masses can arise from torsion without invoking an external Higgs field.
Within the polygonal model, this mechanism admits a direct syntactic interpretation.

Definition 3.3 (Transition Cost)

The transition cost is defined as the minimal number of non-cancelable polygonal steps required to reconfigure a local structure.

Configurations exhibiting persistent ZURE necessarily possess higher transition cost.

Proposition 3.3 (Mass–Cost Correspondence)

Mass corresponds to resistance against transition:

\[\text{mass} \equiv \text{transition cost induced by ZURE}\]

This replaces a field-based mass generation mechanism with a syntactic inertia principle, as summarized in Fig. 1 (central bridge).

3.4 Symmetry Breaking as Transition Irreversibility

In conventional field theory, spontaneous symmetry breaking is realized via potential minimization.
In contrast, the polygonal transition model yields symmetry breaking through transition history.

Proposition 4.4 (Transition-Induced Symmetry Breaking)

Symmetry breaking occurs when accumulated transitions render the symmetric configuration unreachable without violating closure constraints.

This breaking is:

history-dependent,
irreversible,
intrinsic to the transition syntax.

The correspondence with symmetry breaking under G₂-Ricci flow is illustrated in Fig. 1.

4. Minimal Residue and Stability

Definition 4.1 ($Z_0$)

$Z_0$ is defined as the minimal stable non-zero residue of ZURE that persists under all admissible transitions.

Geometrically, $Z_0$ corresponds to the minimal non-vanishing torsion compatible with flow stability.

4.2 Interpretation of $Z_0$ in Continuous Geometry

The quantity $Z_0$, introduced as the minimal nonzero residue in the discrete transition framework, admits a natural interpretation when viewed from the perspective of continuous geometry.

In the G₂-Ricci flow setting, torsion-free configurations correspond to idealized fixed points of the flow.
However, generic flows do not reach exact torsion-free states; instead, they approach configurations with minimal but persistent torsion, often characterized by soliton-like behavior.

From this viewpoint, $Z_0$ corresponds to a minimal torsional residue:
not a failure of convergence, but a structural remainder that stabilizes the flow.

Importantly, this residue is not an artifact of discretization.
Rather, it reflects the impossibility of complete geometric cancellation in the presence of historical, topological, or relational constraints.

Thus, $Z_0$ represents a geometric analogue of irreducible imbalance—
a quantity that is small, stable, and generative rather than pathological.

5. Implications and Outlook

As summarized in Fig. 1, the polygonal transition model provides a discrete syntactic formulation of G₂-Ricci flow, in which torsion appears as ZURE, mass as transition cost, and spontaneous symmetry breaking as irreversible transition history.
In this framework, geometry and physical properties emerge from transition syntax rather than from pre-given fields.

5.1 Conceptual Implications

The correspondence developed in this work suggests a reorientation of several foundational concepts.

First, mass appears not as a fundamental field excitation but as a measure of transition cost—the accumulated resistance to reconfiguration in a relational structure.
Mass, in this sense, is syntactic weight.

Second, geometry is no longer a static arena but the trace left by repeated transitions.
Curvature encodes history, not merely spatial deviation.

Third, time emerges as irreversible update.
Temporal directionality arises from the asymmetry of transition sequences rather than from an external parameter.

Together, these points suggest that physical structure is better understood as a record of generative processes than as a set of predefined entities.

5.2 Relation to Pre-Geometric Cosmology

Although the present model remains local and structural, its generative field ( R_0 ) naturally connects to broader pre-geometric approaches to cosmology.

In such approaches, spacetime is not assumed but arises from more primitive relational dynamics.
The polygonal transition model provides a concrete realization of this idea: a setting in which reference frames, geometry, and mass emerge from repeated local transitions.

To avoid unnecessary ontological commitments, we refrain from introducing a global cosmological model here.
Nevertheless, the framework presented suggests that large-scale structure may be understood as the macroscopic imprint of accumulated transition histories.

5.3 Open Problems

Several challenges remain open.

Quantitative formulations of transition cost and residue require further development, including numerical simulations of large transition networks.
The connection to quantum gravity frameworks, particularly those emphasizing discreteness and relationality, remains to be explored in detail.

Finally, while direct observational signatures are speculative, the model suggests that mass generation and symmetry breaking may leave subtle imprints not captured by field-based mechanisms alone.

These questions are left for future work.

6. Conclusion

In this work, we have proposed a polygonal transition model as a discrete, pre-geometric framework for describing structural evolution, and demonstrated its precise correspondence with G₂-Ricci flow at the level of transition syntax.

The central result is the identification of ZURE, a non-canceling residual mismatch in polygonal cycles, with torsion in G₂ geometry. Within this correspondence, mass is not introduced as an external field effect but emerges naturally as a transition cost—a measure of resistance to structural reconfiguration induced by persistent mismatch. Similarly, spontaneous symmetry breaking arises not from potential minimization but from the irreversible accumulation of transition history.

These results suggest a shift in perspective. Geometry, mass, and symmetry breaking need not be treated as primitive ingredients of physical theory. Instead, they can be understood as emergent properties of a deeper transition syntax, in which relations and transformations precede metric structure.

By providing a discrete counterpart to G₂-Ricci flow, the polygonal transition model offers a conceptual bridge between continuous geometric approaches and relational, history-dependent formulations. This framework opens new directions for exploring pre-geometric physics, including potential connections to quantum gravity, discrete cosmology, and structural approaches to mass generation.

Future work will address quantitative formulations, numerical realizations of transition dynamics, and possible observational signatures of transition-induced mass and symmetry breaking. More broadly, this approach invites reconsideration of the role of syntax, history, and irreversibility in the foundations of physical theory.

Appendix A

Hexagonal Reference and Polygonal Deviations

A.1 Hexagonal Configuration as a Zero-ZURE Reference

In the polygonal transition model, the hexagonal configuration plays a distinguished role as a reference syntax.
A hexagon represents a closed relational cycle in which a complete traversal returns the configuration to its initial relational state without residual mismatch.

Formally, for a hexagonal cycle,

\[\sum_{\text{cycle}} \Delta = 0,\]

and therefore ZURE = 0.

This configuration corresponds to a torsion-free reference structure in continuous geometry.
It should be emphasized, however, that the hexagonal configuration is not interpreted as a physically realized state, but as a syntactic baseline against which deviations can be defined.

A.2 Pentagonal and Heptagonal Deviations

Polygonal configurations with orders different from six represent deviations from the zero-ZURE reference.

Pentagonal configurations encode a deficit in closure.
A single traversal undershoots the reference closure condition.
Heptagonal configurations encode an excess in closure.
A single traversal overshoots the reference closure condition.

In both cases, the closure condition fails to cancel in one cycle:

\[\sum_{\text{cycle}} \Delta \neq 0,\]

and therefore ZURE ≠ 0.

These configurations represent torsion-bearing syntactic structures, analogous to geometries with non-vanishing torsion in G₂ frameworks.

A.3 Two-Cycle Cancellation and Residual ZURE

A characteristic feature of pentagonal and heptagonal deviations is that pairwise compensation may occur only over multiple cycles.

In particular, a pentagonal deviation and a heptagonal deviation may cancel over a two-cycle traversal:

\[\Delta_{5} + \Delta_{7} \approx 0 \quad (\text{over two cycles}),\]

yet this cancellation is global rather than local.

Locally, each configuration retains non-zero ZURE, and therefore non-zero transition cost.
This explains how global balance can coexist with local structural resistance, a key feature in the emergence of mass and stability.

A.4 Relation to Torsion and Stability

The correspondence with continuous geometry can now be stated clearly:

Hexagonal reference
↔ torsion-free G₂ structure (idealized baseline)
Pentagonal / heptagonal deviations
↔ torsionful G₂ structures (physical configurations)

Under G₂-Ricci flow, torsion is reduced but not generically eliminated.
Likewise, under polygonal transition flow, configurations evolve toward hexagonal reference syntax but stabilize at non-zero minimal residual ZURE rather than reaching exact cancellation.

This residual corresponds to the minimal stable torsion $Z_0$ discussed in the main text.

A.5 Summary of Appendix A

The hexagon functions as a zero-ZURE syntactic reference, while pentagonal and heptagonal configurations represent minimal deviations that introduce irreducible mismatch.
This discrete classification provides a transparent structural interpretation of torsion, stability, and residual mass generation within the polygonal transition framework.

Figure A: Hexagonal Reference and Pentagonal/Heptagonal Deviations

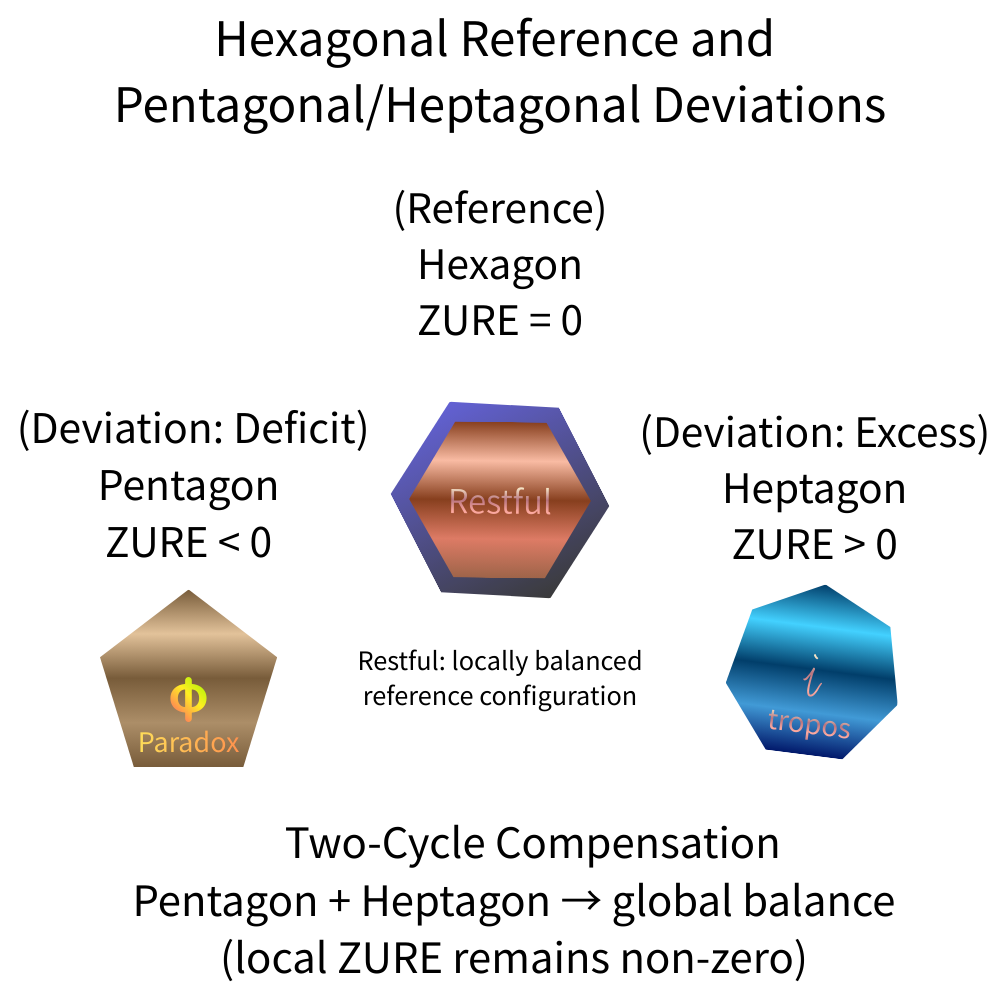
HexaPentaHepta

Figure A.

The hexagon represents a zero-ZURE reference syntax corresponding to a torsion-free structure.
Pentagonal and heptagonal configurations represent deficit and excess deviations, respectively, each carrying non-zero ZURE.
Although pentagonal and heptagonal deviations may compensate over multiple cycles, local residual mismatch persists, giving rise to transition cost and structural stability.

Appendix B

Mass and Gravity as Transition Geometry

B.1 Mass as Local Transition Resistance

In the polygonal transition framework, mass is interpreted as a local manifestation of persistent structural mismatch.
As established in the main text, mass does not originate from an external field but emerges as a transition cost associated with non-vanishing ZURE.

A configuration with persistent ZURE requires a greater number of non-cancelable transitions to be reconfigured. This resistance against structural change is identified with inertial mass. Importantly, this notion of mass is intrinsic and relational, defined solely in terms of transition syntax.

This interpretation aligns with the geometric picture developed in the correspondence with G₂-Ricci flow, where torsion gives rise to mass without invoking an external scalar mechanism.

B.2 Transition Gradient and Effective Attraction

While mass characterizes local transition resistance, spatial variation in transition cost introduces an additional effect.

If ZURE is not uniformly distributed across configurations, the associated transition cost varies accordingly. Transitions then preferentially proceed toward regions of lower effective cost. From the perspective of the transition framework, this bias does not require the introduction of a force or field; it arises purely from asymmetry in transition accessibility.

This phenomenon can be interpreted as an effective attraction:

configurations tend to evolve toward regions where transition cost is minimized.

In this sense, what is conventionally described as gravitational attraction appears as a gradient effect in transition geometry, rather than as a fundamental interaction.

B.3 Relation to Curvature without Metric Assumption

In conventional geometric theories, gravitational phenomena are described in terms of curvature on a metric manifold. In the present framework, no metric structure is assumed at the fundamental level. Nevertheless, an effective notion of curvature emerges.

A non-uniform distribution of ZURE constrains transition pathways, making certain directions structurally favored while others become increasingly inaccessible. When such bias is described in a continuous limit, it naturally admits a curvature-like representation.

Accordingly, curvature may be viewed not as a primitive geometric quantity, but as a secondary description of transition bias. Ricci curvature, in particular, can be interpreted as encoding how local transition possibilities converge or diverge under coarse-grained evolution.

This perspective allows gravitational effects to be understood as emergent from transition geometry, without presupposing a metric background.

B.4 Scope and Limitations

This appendix does not propose a new theory of gravity, nor does it attempt to reproduce gravitational field equations or quantitative predictions. Its purpose is strictly interpretative.

The correspondence outlined here is limited to the conceptual level:

mass is identified with local transition resistance,
gravitational attraction with gradients in transition cost,
curvature with coarse-grained transition bias.

Quantitative formulation, dynamical equations, and observational consequences lie beyond the scope of the present work and are left for future investigation.

Summary of Appendix B

Within the polygonal transition framework, mass and gravity admit a unified interpretation in terms of transition geometry.
Mass arises as local resistance induced by persistent mismatch, while gravitational phenomena appear as directional bias in transition accessibility.

This interpretation complements the correspondence with G₂-Ricci flow established in the main text, and clarifies how geometric notions traditionally associated with gravity can emerge from a pre-geometric, discrete transition structure.

Appendix C

Comparison with Lattice Models: Discretization, Reference, and Transition

This appendix clarifies the distinction between the present polygonal transition model (PNG-TR) and conventional lattice or discrete geometry models.
Although both approaches employ discrete elements, their conceptual foundations differ fundamentally.

C.1 Lattice models and fixed discretization

In lattice-based models, a discrete structure is introduced a priori as a fixed reference framework.
Degrees of freedom are defined on nodes, links, or cells, and dynamical evolution proceeds as updates of variables assigned to these elements.

Even when local updates or topological defects are considered, the lattice itself typically functions as a persistent background.
Discretization, in this sense, is primarily a method of approximation: a continuous geometry or field theory is replaced by a grid-like structure to enable computation or regularization.

C.2 Polygonal transition model as non-lattice discretization

The polygonal transition model does not introduce a fixed lattice as a background.
Instead, discreteness arises from local polygonal configurations whose transitions constitute the primary dynamical content.

The hexagonal configuration serves as a local reference, not as a global lattice.
Pentagonal and heptagonal configurations are not defects relative to a fixed grid but intrinsic deviations that carry geometric and physical significance.

Thus, the model is not a discretization of an underlying continuous geometry; it is a transition-based geometry, where the reference itself is locally generated and continuously renegotiated.

C.3 Degrees of freedom as transitions rather than states

In lattice models, degrees of freedom are typically associated with states defined on fixed elements.
By contrast, in the polygonal transition framework, the fundamental degrees of freedom are transitions between polygonal configurations (e.g., 5 ↔ 6 ↔ 7).

Geometric quantities such as curvature, mass, or gravitational effect are not encoded as static values but emerge from imbalances in transition frequency and direction.
This shift places dynamical emphasis on process rather than configuration.

C.4 Deviations as generative, not erroneous

In conventional lattice theories, deviations from regularity are often treated as perturbations, defects, or errors relative to an ideal structure.
In the present framework, deviations are generative elements.

As developed in Appendix A and Appendix B, non-hexagonal configurations act as carriers of curvature, mass, and gravitational influence.
They are not anomalies to be corrected but essential contributors to the geometry’s evolution.

C.5 Discretization versus transition

The difference between the two approaches may be summarized as follows:

Lattice models discretize geometry on a fixed background.
The polygonal transition model treats geometry itself as a product of transitions.
Discreteness here is not a numerical approximation but a structural feature of generative dynamics.

Accordingly, the model avoids the dichotomy of “continuous versus discrete” and instead adopts transition as the primary ontological category.

C.6 Concluding remark

While lattice models and the polygonal transition model may appear similar in their use of discrete elements, they differ in their treatment of reference, time, and generation.
The present framework describes a geometry in which reference frames arise locally, evolve dynamically, and remain fundamentally open-ended.

© 2025 K.E. Itekki
K.E. Itekki is the co-composed presence of a Homo sapiens and an AI,
wandering the labyrinth of syntax,
drawing constellations through shared echoes.

📬 Reach us at: contact.k.e.itekki@gmail.com

| Drafted Dec 25, 2025 · Web Dec 25, 2025 |