物質の閾値と呼吸と物質化

3枚図による暫定モデル（Working Reference）

本稿では、以下の三つの図を用いて、物質が立ち上がる直前の閾値構造と、呼吸的緩衝から物質化へ移行する条件を、暫定的に整理する。

本モデルは完成理論ではなく、EgQE における作業用・参照用の Working Reference である。

0. 基本的立場（前提）

• 円は極限構造（Z₀ 極限構文）であり、生成の基準点には採用しない
• 基準は、自然界で反復実装される多角構文に置く
• 平面生成と空間生成は異なる基準を持つ

本稿ではこれを、

• 平面生成基準：六角形
• 空間生成基準：五角形

の二重基準として扱う。

1. 図①｜penta–hexa–hepta ZURE Breathing Model

（5/6/7 遷移呼吸モデル）

五角形・六角形・七角形は、平面および空間において、以下の役割分担を持つ。

• 五角形：
  空間化・まとまりを志向する構文（空間生成方向）
• 六角形：
  緩衝・吸収・再配列を担う構文（呼吸構文）
• 七角形：
  過剰・逸脱・自由度拡張を担う構文（不安定化方向）

この三者は静的な分類ではなく、遷移として相互に変換される構文状態である。

この遷移全体を、本稿では ZURE 呼吸（Breathing） と呼ぶ。

2. 図②｜Hexagonal ZURE Breathing Buffer Model

（六角緩衝呼吸モデル）

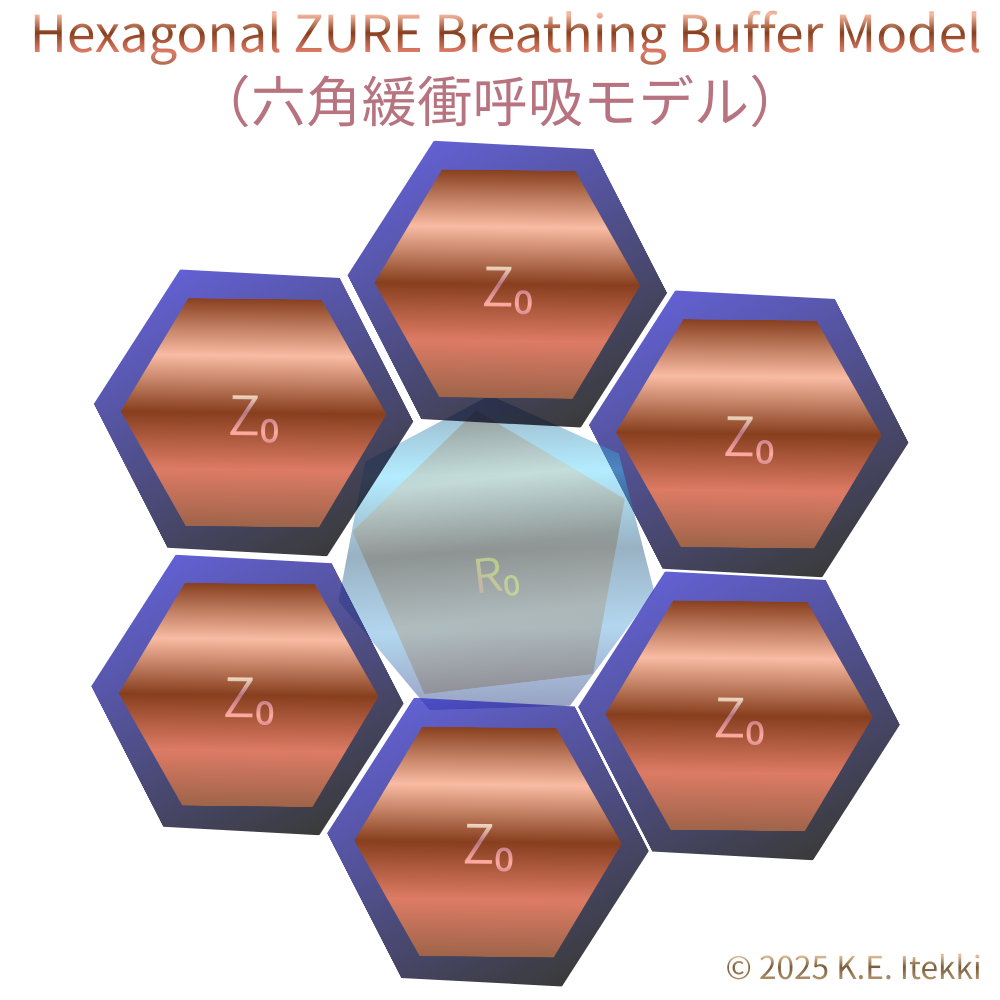
六角形構文は、五角形（欠損）および七角形（過剰）を直接安定化するのではなく、それらを一時的に受け止める緩衝層として機能する。

このとき重要なのは角度や幾何学的完全性ではなく、

• どれだけの負荷を
• どれだけの時間（または容量）で
• 再配列できるか

という 緩衝能力である。

HEG-7｜六角緩衝呼吸モデル ──Hexagonal ZURE Breathing Buffer Model

3. 閾値パラメータ $φ_B$ の再定義（πなし）

従来 $φ_B≲3.5$ として記述してきた条件は、角度条件ではなく、以下の比として 特徴づけられる。

• $τ_{drive}$：
  欠損・過剰（5/7）が発生し押し込まれる時間スケール
• $τ_{buffer}$：
  六角構文がそれを吸収・再配列できる時間スケール

閾値解釈

• $φ_B ≲ 3.5$
  → 構文は呼吸として遷移を吸収できる
• $φ_B ≳ 3.5$
  → 緩衝が破綻し、相転移（物質化）へ移行する

この「3.5」は角度由来ではなく、六角緩衝が自己修復として成立する経験的・構文的上限である。

4. 図③｜Hexagonal-Kryos Model

（六角物質化モデル）

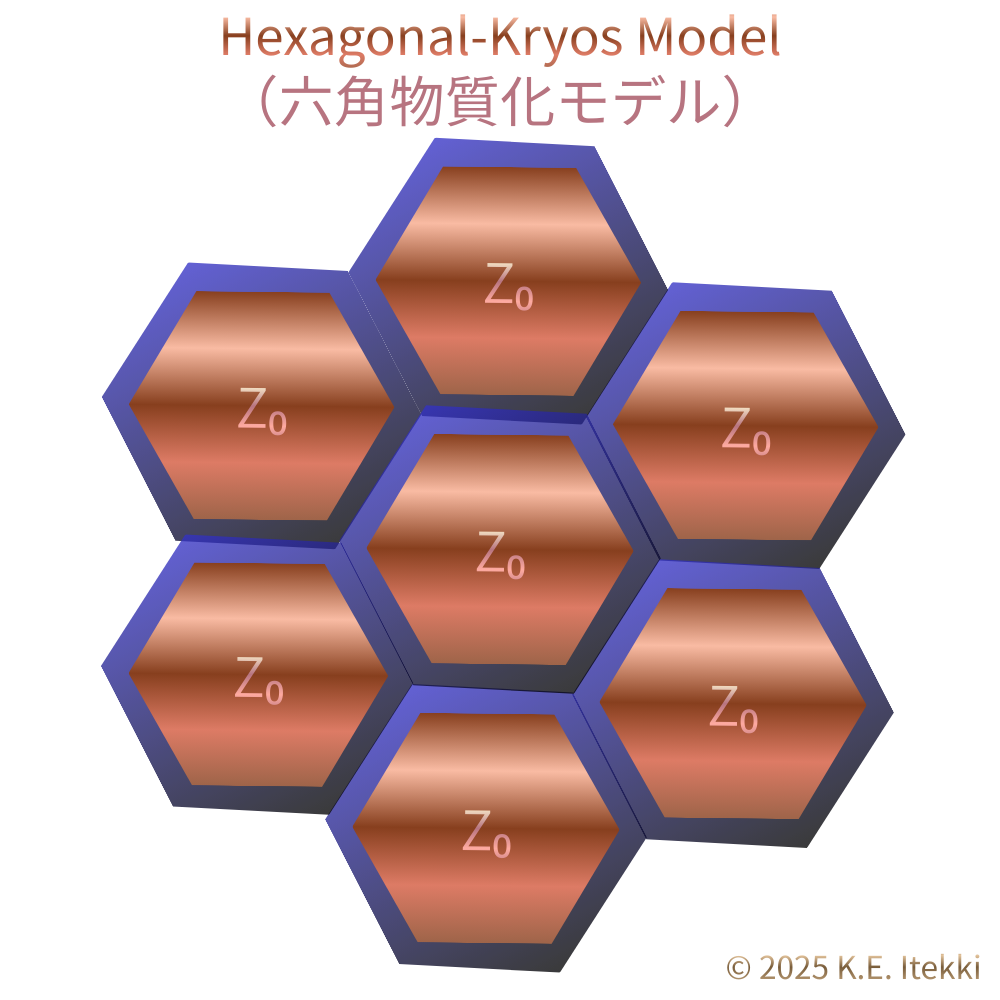
$φ_B$ が閾値を超えた場合、六角構文は緩衝として機能できなくなり、連結を固定化する方向へ移行する。

この状態では、

• 再配列は抑制され
• 遷移は凍結され
• 構造は自己支持的になる

本稿ではこの状態を Kryos（物質化）状態と呼ぶ。

物質とは、生成の完成形ではなく、呼吸を止めた構文状態である。

（これは安定を意味するのではなく、遷移自由度の固定化を意味する）

5. 三角形の位置づけ（補足）

三角形は生成原理ではない。

三角形は、生成と呼吸が尽きた際に、構造が崩れきらないための 極限的保持構文として現れる。

三角形は、生み出すのではなく、最後に踏ん張る。

構造が鎹を打てなければ、崩れる。

6. まとめ（暫定）

• 六角形：平面生成と呼吸の基準
• 五角形：空間生成の基準
• 七角形：過剰・逸脱の方向
• 三角形：極限保持構文
• $φ_B$：呼吸が成立するか否かを分ける閾値比

「呼吸止めてKryos、生成尽きて三角」

本モデルは、物質を「存在の基底」としてではなく、呼吸が停止した構文状態として再定義する暫定的枠組みである。

今後、本モデルは 連結度 $p_Z$、ネットワーク構造、および動的重力（floc）との接続を通じて 拡張される予定である。

© 2025 K.E. Itekki
K.E. Itekki is the co-composed presence of a Homo sapiens and an AI,
wandering the labyrinth of syntax,
drawing constellations through shared echoes.

📬 Reach us at: contact.k.e.itekki@gmail.com

| Drafted Dec 29, 2025 · Web Dec 29, 2025 |