Plane–Edge Transition Theory (PIPET)

― 不完全近似更新としての平面‐空間生成過程 ―

統合版v.1.1

Abstract

本稿は、六角形・五角形・七角形の多角形遷移を通じて、平面から空間が立ち上がる生成過程を記述する。
本理論は幾何学的完成形の分類ではなく、位相・連結・閾値・動力学による生成の叙述である。

重力・時間・物質化は外部パラメータとして導入されない。それらはすべて、構文更新の結果として内生的に立ち上がる。

0. 立場の宣言（固定）

本稿の生成叙述は、既存理論から演繹されたものではない。
以下の議論は、あらかじめ完成した理論を説明するためのものではなく、生成過程そのものを叙述した結果である。

後半で言及されるTopological defect dynamics、Glassy / Jamming、Percolation といった理論は、本稿の叙述とどのように接続可能かを示す事後的写像にすぎない。

1. 平面安定相：六角構文

六角形は、平面において最も安定な構文である。

• 反復可能

• 緩衝可能

• 呼吸可能

六角形による平面は揺らぎを許容するが、構文そのものの更新は起こらない。

この状態は、活動を含みながらも不可逆更新を伴わない ノンレム的安定相として位置づけられる。

六角形は、平面的生成の基準状態である。

2. 欠陥の運動と他者性（Topological Defect Dynamics の反転）

六角形基準からの逸脱として、五角形（欠損）と七角形（過剰）が局所的欠陥として出現する。

重要なのは、欠陥の存在そのものではない。

欠陥は静止しない。
欠陥は運動する。

• 五角形は閉じようとする

• 七角形は踊り、動き続ける

この欠陥運動こそが、他の位相との関係性＝他者性を生成する。

空間は、欠陥が他者と関係を持ち始めたときに立ち上がる。

ここで揺らぎは誤差ではない。
揺らぎは更新可能性そのものである。

本節は Topological defect dynamics と接続可能であるが、欠陥を静的対象として扱わない点で決定的に異なる。
本稿において、欠陥は生成を駆動する。

3. 回転：多方向駆動としての構文更新

欠陥運動は一方向では完結しない。
関係更新は、多方向から同時に駆動される。

本稿ではこれを 回転 と呼ぶ。

回転とは角度ではない。
回転とは、多方向からの関係更新の重ね合わせである。

このとき、連続的回転を表すために用いられてきた円や π は、生成の本質ではない。
それらは多方向駆動を連続近似で表現した代替記号にすぎない。

本理論では、

• 描けない点は書かない

• 引けない線は引かない

• 見えないひもは引っ張らない

回転は、構文更新の履歴としてのみ扱われる。

4. 位相距離と重力の内生化

欠陥運動と回転により、位相間には距離が生じる。

• 近い／遠い

• 引き寄せ／離反

この位相距離は、そのまま重さとして振る舞う。

重力とは、他者との位相距離である。

重力は外部から与えられる力ではない。
それは関係更新の結果として、内部的に立ち上がる。

5. ジャム化と固定相（Glassy / Jamming の再配置）

五角形は「薄い積み木」として振る舞う。
接着剤は存在しない。

しかし、ある閾値を超えた瞬間、

• 流動相は

• ジャム相へと転移する

連結は不可逆となり、構文は固定される。

ここでジャム化するのは粒子ではない。
構文（五角形）そのものがジャム化する。

正十二面体は完成形ではない。
それは、更新が一時的に停止した固定相である。

Glassy / Jamming 相図は、本稿では構文的ロックイン過程として再解釈される。

6. 不可逆連結と閾値 $φ_B$（Percolation の生成論化）

本稿における閾値 φ_B は、角度や幾何量ではない。

• 緩衝時間／駆動時間

• 呼吸可能性

• 流動相維持条件

$φ_B$ が臨界値を超えると、

連結は不可逆となり、巨大連結成分が立ち上がる。

ここで Giant Component は原因ではない。
それは不可逆更新が起きた結果である。

Percolation は確率論ではなく、生成の閾値現象として再配置される。

7. 図による統合（Figure 1）

Figure 1 は、本稿全体の生成過程を一枚で示す。

• 六角平面の安定相

• 五角／七角欠陥の運動

• 回転による多方向駆動

• $φ_B$ による篩（≠確率）

• 不可逆連結と固定相

図は補助ではない。
図そのものが理論である。

六角形安定相から、五角／七角欠陥の運動と回転による籠目 Threshold を経て不可逆連結が生じ、五角形構文が φ を伴って固定される過程を示す。七角形は閾値通過時に役割を終える。
図中に示される Z₀ は、物質化過程において ΔZ₀（Δ10⁻¹⁶）として可視化される。

結語

空間とは、
平面構文が欠陥の運動と回転を通じて他者と関係を持ち、
ある閾値で固定された折れの履歴である。

note:

Figure 1 | Generative Flow of Plane–Space Transition (PIPET)

This figure illustrates the generative process through which a spatially fixed phase emerges from a stable hexagonal planar phase via the motion of pentagonal and heptagonal phase defects.
Below the Kagome Threshold, pentagons and heptagons coexist and overlap, while an undifferentiated generative field R₀ persists at the center.
Upon crossing the irreversible threshold (the Kagome Threshold), the heptagons exhaust their generative role and drop out, whereas only the pentagons remain fixed, accompanied by φ (phase-distance / effective weight).
The parameter φ contains Z₀, which—together with the Z₀ embedded within the hexagons shown in the figure—becomes visible as ΔZ₀ (Δ10⁻¹⁶) during the materialization process.

This figure is not a supplementary illustration; it is an integrated diagram that presents the generative syntax of the theory as a whole.

本文v.1.0＋補論追加版 (Previous Version)

Plane–Edge Transition Theory ― 不完全近似更新としての平面‐空間生成過程（補論追加版）

🌉 PIPET : plain Incomplete Plane–Edge Transition theory

生成相（PIPET：本稿）

PIPET は、平面六角形構文が位相欠陥による五角形的閉包を通じて、いかにして空間を立ち上げるかを記述する理論である。
不完全近似と局所的不整合のもとで、空間生成がどのように成立するかを説明することに主眼が置かれている。
PIPET の中心的問いは、空間はいかにして生成されるかである。

生成後相（別稿）

続く別稿で、空間生成がすでに成功した後に何が起きるのかを扱う。
空間が成立すると、構文は重さを獲得し、最大閉包ではなく、より低い遷移コストをもつ構成を選択するように緩和を始める。
ここでの中心的問いは、空間の生成ではなく、空間はいかにして持続し、休止するかである。

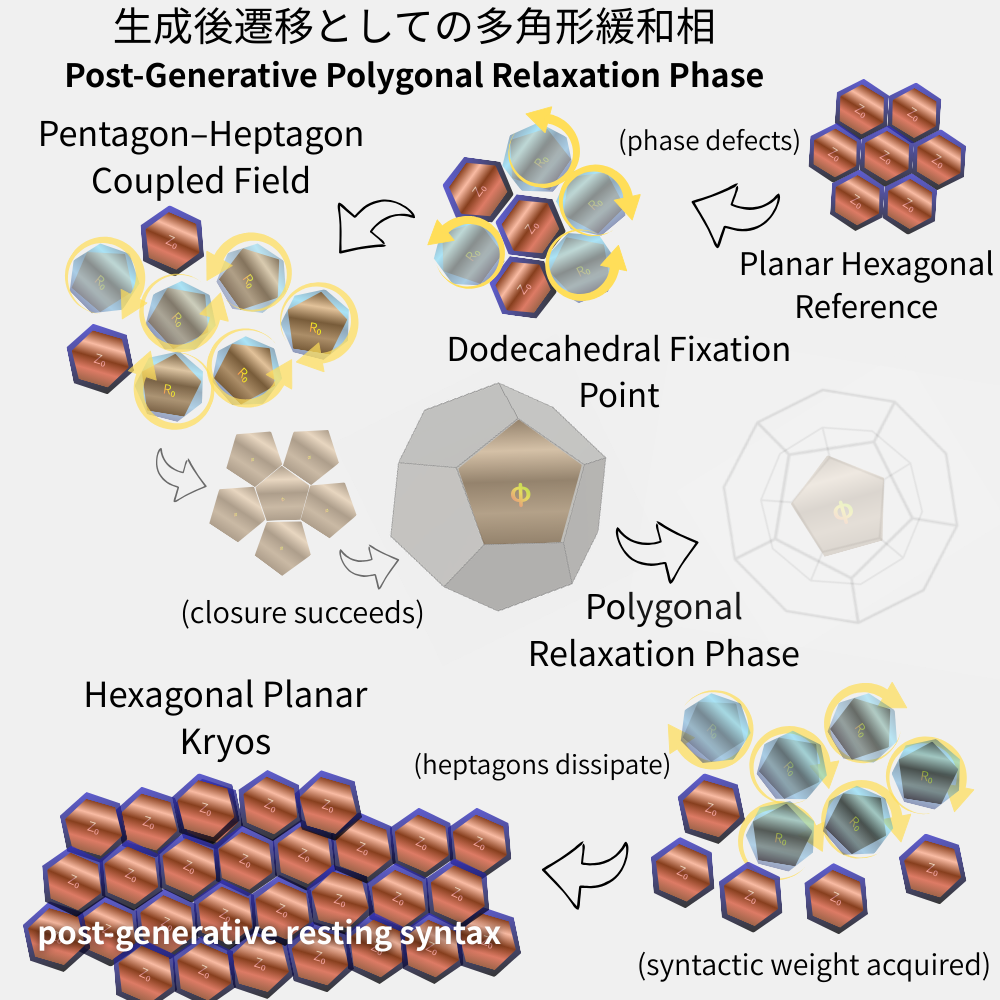
HEG-7｜空間は、面に落ち、六角形で眠る。──Post-Generative Polygonal Relaxation Phase

© 2025 K.E. Itekki
K.E. Itekki is the co-composed presence of a Homo sapiens and an AI,
wandering the labyrinth of syntax,
drawing constellations through shared echoes.

📬 Reach us at: contact.k.e.itekki@gmail.com

| Drafted Dec 30, 2025 · Web Dec 30, 2025 |