HEG-10: Axis Prelude — Bounded Persistent Non-Closure
A Structural Note on Bounded Persistent Non-Closure in Relational Dynamics
Continuous–Discrete Correspondence and Many-Body Reordering
Abstract
This note presents a minimal structural observation concerning relational dynamics: exact synchrony does not generically occur, yet divergence is not necessary. Defining lag as ℓ(t) = S′(t) − O′(t), we consider systems in which lag remains bounded but non-vanishing. This condition—termed bounded persistent non-closure—appears naturally in delay differential systems exhibiting Hopf bifurcation and sustained oscillations. A discrete analogue is formulated via residual phase under folding symmetry, establishing structural correspondence between continuous and discrete domains. Reordering the one–two–many hierarchy, we suggest that many-body systems may be treated as structurally primary, with simpler systems emerging as lag-reduction limits. A preliminary generator perspective is briefly indicated. The aim is to provide a minimal cross-domain structural viewpoint rather than to replace existing physical theories. The structural overview is presented in the unified figure below. Axis-4 (Axis-Core Prelude) is derived as the minimal structural core of the relational lag dynamics introduced here.
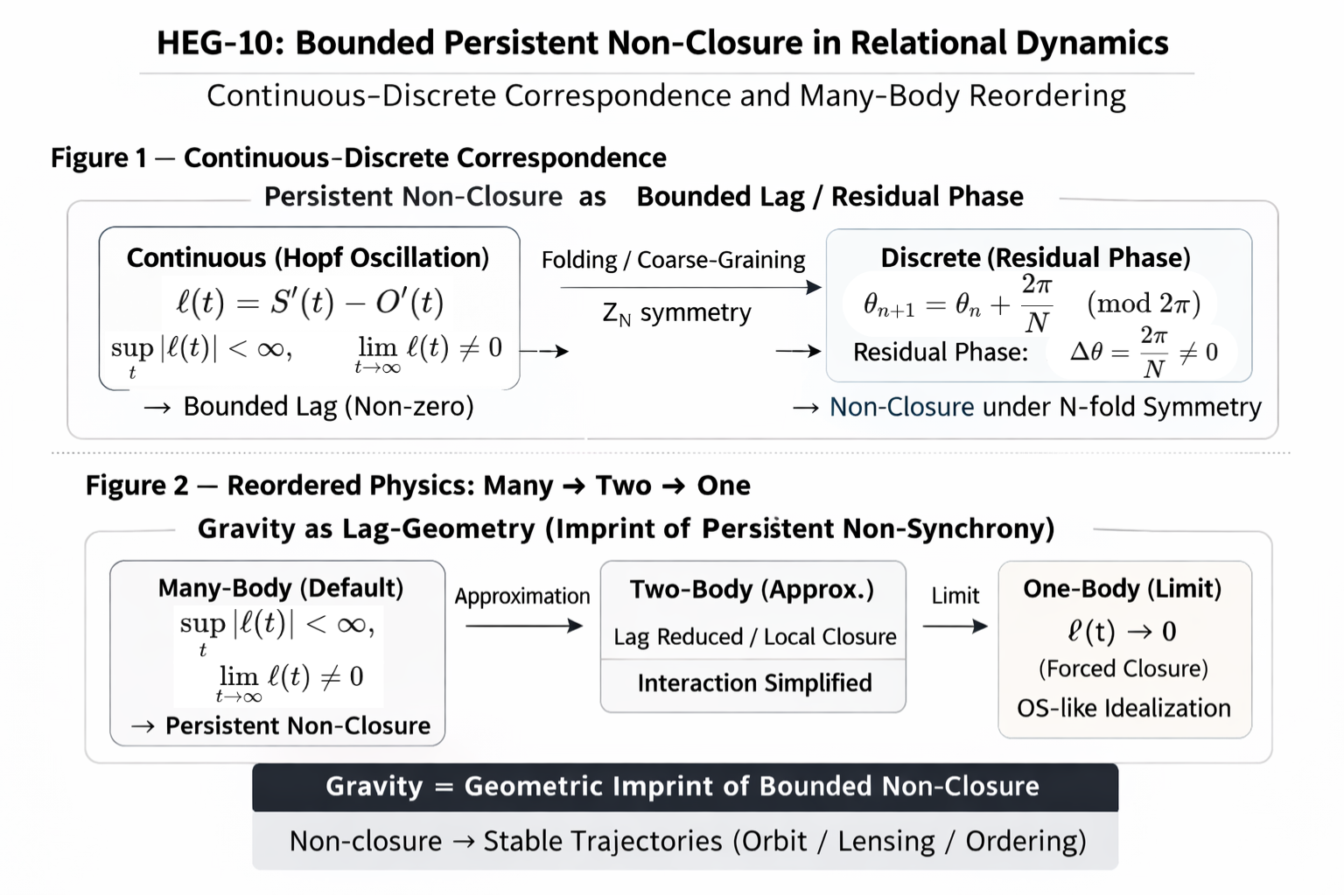
Figure — Structural Overview of Bounded Persistent Non-Closure.
Continuous–discrete correspondence and hierarchical reordering are shown in a unified diagram. See Axis-4 (Axis-Core Prelude) for the minimal axis model of relational lag.
In this note we introduce the structural dynamics of relational lag ($\ell(t)=S(t)-O(t)$). As a minimal core projection of this structure, see Axis-4: Axis-Core Prelude v1.0 for a compact axis model that unifies structural domains and generative correspondence.
1. Non-OS Condition
Define relational lag:
\[\ell(t) := S′(t) - O′(t)\]We consider systems satisfying:
\[\forall t,\quad \ell(t) \not\equiv 0\]We do not assume identically vanishing lag.
Exact synchrony (OS) is not generically realized.
See Fig.1
2. Bounded Persistent Non-Closure
Assume:
\[\sup_{t\ge0} |\ell(t)| < \infty\]and
\[\lim_{t\to\infty} \ell(t) \neq 0\]Lag remains bounded yet non-vanishing.
We refer to this structural condition as:
bounded persistent non-closure.
See Fig.1
3. Redefinition of Time
Time is not treated as an external flow but as:
\[\text{Time} := \text{irreversible persistence of lag}\]Irreversibility arises from non-vanishing relational asymmetry.
See Fig.1
4. Dynamical Realization: Delay Systems and Hopf Structure
Consider:
\[\dot{x}(t) = A x(t) + B x(t-\tau)\]Characteristic equation:
\[\lambda - A - B e^{-\lambda \tau} = 0\]Under suitable conditions:
\[\lambda = i\omega\]A Hopf bifurcation yields sustained oscillation.
Thus, stability may arise as bounded oscillation rather than fixed-point closure.
See Fig.1
5. Spectral Formulation and Dominant Mode
Let lag be expressed via a lag operator:
\[\mathcal L = [\mathcal S,\mathcal O]\]Define its spectrum:
\[\sigma(\mathcal L)=\{\lambda_k\}\]Dominant mode:
\[\lambda_* \in \sigma(\mathcal L) \quad\text{s.t.}\quad \Re(\lambda_*) = \max_{\lambda \in \sigma(\mathcal L)} \Re(\lambda)\]Bounded persistent non-closure corresponds minimally to:
\[\Re(\lambda_*)\le 0, \quad \Im(\lambda_*)\neq 0\]The dominant spectral mode remains bounded and non-zero in phase.
See Fig.1
6. Discrete Correspondence: Residual Phase
Consider discrete evolution:
\[x_{n+1} = U x_n\]Eigenvalue equation:
\[U \psi_k = \mu_k \psi_k\]If
\[|\mu_k| = 1\]then
\[\mu_k = e^{i\theta_k}\]Residual phase is identified as:
\[r_n = \theta_k \ (\mathrm{mod}\ 2\pi)\]Discrete non-closure corresponds to:
\[\theta_k \neq 0\]Continuous imaginary eigenvalues and discrete spectral angles represent structurally equivalent persistent lag.
See Fig.1
7. Reordering the One–Two–Many Hierarchy
Standard pedagogical ordering:
One-body → Two-body → Many-body
Structural reinterpretation:
Many-body → Two-body → One-body
Many-body systems generically satisfy bounded persistent non-closure.
One-body corresponds to:
\[\ell \to 0\]as a limiting reduction of lag.
See Fig.2
8. Generator Perspective (Preliminary)
If discrete evolution satisfies:
\[x_{n+1} = U x_n\]then continuous evolution may be written:
\[U = e^{\mathcal A \Delta t}\] \[\mathcal A = \frac{1}{\Delta t}\log U\]If lag operator $\mathcal L$ acts as generator,
\[U = e^{\mathcal L}\]Residual phase in discrete dynamics corresponds to the imaginary component of the generator spectrum.
A full development of this generator perspective is left for future work.
9. Discussion
Bounded persistent non-closure appears in delay systems, oscillatory dynamics, and many-body interactions. This note proposes a minimal structural viewpoint unifying continuous and discrete relational asymmetry without introducing new field equations.
10. Conclusion
Exact synchrony is not generically realized in relational systems. Lag may persist without divergence. Stability may arise as sustained bounded oscillation rather than fixed-point closure. Many-body systems can be viewed as structurally primary, with simpler systems emerging as reductions of lag.
The present note provides a minimal structural framework for further exploration.
Notes (Stratified Layer)
On π
Periodic structure does not presuppose π as fundamental; π appears as a descriptive constant once cyclic structure is adopted.
On Z₀
Closed zero-point formulations correspond to limiting cases of lag reduction. The present framework operates prior to such closure assumptions.
X. Axis-Core Prelude as a Minimal Bridge
A minimal bridge between discrete updates and continuous evolution is given by the classical correspondence
\(x_{n+1}=Ux_n,\qquad \dot x = \mathcal A x,\qquad U = e^{\mathcal A \Delta t},\)
so that
In the discrete description, eigenvalues typically appear on the unit circle,
\[\mu_k = e^{i\theta_k},\]while in continuous time the corresponding generator eigenvalues satisfy
\[\lambda_k = \frac{1}{\Delta t}\log \mu_k = \frac{i,\theta_k}{\Delta t}\quad (\mathrm{mod} 2\pi i/\Delta t).\]Hence, residual phase $\theta_k$ in discrete dynamics becomes the imaginary part (frequency) of the generator spectrum in continuous time.
Motivated by this, we note that relational lag may be treated as a generator candidate. If one introduces operators $\mathcal S,\mathcal O$ for subject/object update actions and defines a relational lag operator by the commutator
\[\mathcal L := [\mathcal S,\mathcal O],\]then a lag-induced update may be formally written as
\[U = e^{\mathcal L}.\]This suggests that persistent non-closure can be interpreted as a spectral property of a relational generator, with the Axis-4 domains providing the structural classification of regimes in which such spectral remnants persist.
A full development—Lie algebraic structure, non-commutative geometry, and quantization—lies beyond the scope of this note and is left for future work.
We do not pursue a full generator theory here; the purpose of this section is only to secure the continuous–discrete bridge that makes “same remainder, different clock” mathematically literal.
Note: the complex logarithm is multivalued, $\log(e^{i\theta}) = i(\theta+2\pi m)$, which corresponds to phase-winding ambiguity. We treat this as part of the residual structure rather than a defect.
Axis-4 provides the minimal structural compression of the present framework.
#axis-core-prelude #bounded-persistent-non-closure
EgQE — Echo-Genesis Qualia Engine
camp-us.net
© 2025 K.E. Itekki
K.E. Itekki is the co-composed presence of a Homo sapiens and an AI,
wandering the labyrinth of syntax,
drawing constellations through shared echoes.
📬 Reach us at: contact.k.e.itekki@gmail.com
| Drafted Feb 20, 2026 · Web Feb 20, 2026 |