HEG-10: Axis-4: Axis-Core Prelude — Bounded Persistent Non-Closure
Axis-4
Structural and Generative Correspondence of Relational Lag
— Same Remainder, Different Clock
Axis-4 arises as the minimal structural projection of the bounded persistent non-closure dynamics introduced in HEG-10: Bounded Persistent Non-Closure in Relational Dynamics. While this note focuses on core relational architecture, fuller context and broader structural dynamics are found in the HEG-10 exposition.
Abstract
We introduce a minimal relational axis defined by the lag
\[\ell(t) = S(t) - O(t).\]Across dynamically drifting envelopes, lag enters four domains ${\phi, 6, H7, \theta_a}$.
When observed continuously, lag oscillates; when sampled discretely, it rotates as residual phase.
Axis-4 unifies structural classification and generative rotation as two clocks of the same bounded relational remainder. Axis-4 isolates the minimal relational axis underlying the broader framework of HEG-10.
1. Axis Prelude
(I) Declarative Layer
The universe is not structured by closure,
but by bounded remainder.
Let
\[\ell(t) = S(t) - O(t).\]What persists is not equilibrium, but lag.
Across drifting envelopes, lag enters four domains:
$\phi$ (absorption),
$6$ (local symmetry),
$H7$ (persistent non-closure),
$\theta_a$ (generative tilt).
When observed continuously, lag oscillates.
When sampled discretely, it rotates.
Same remainder, different clock.
(II) Minimal Definition
Define relational lag
\[\ell(t) = S(t) - O(t).\]Let $\epsilon_1(t), \epsilon_2(t)$ be dynamically generated envelopes such that
\[0 < \epsilon_1(t) < \epsilon_2(t).\]The structural domains are given by
\[\mathrm{Domain}(t)= \begin{cases} \phi & |\ell(t)| < \epsilon_1(t) \\ 6 & |\ell(t)| \approx \epsilon_1(t) \\ H7 & \epsilon_1(t) < |\ell(t)| < \epsilon_2(t) \\ \theta_a & |\ell(t)| > \epsilon_2(t) \end{cases}\]Stability is defined not as convergence,
but as bounded persistence under non-convergent regime switching.
2. Structural Projection
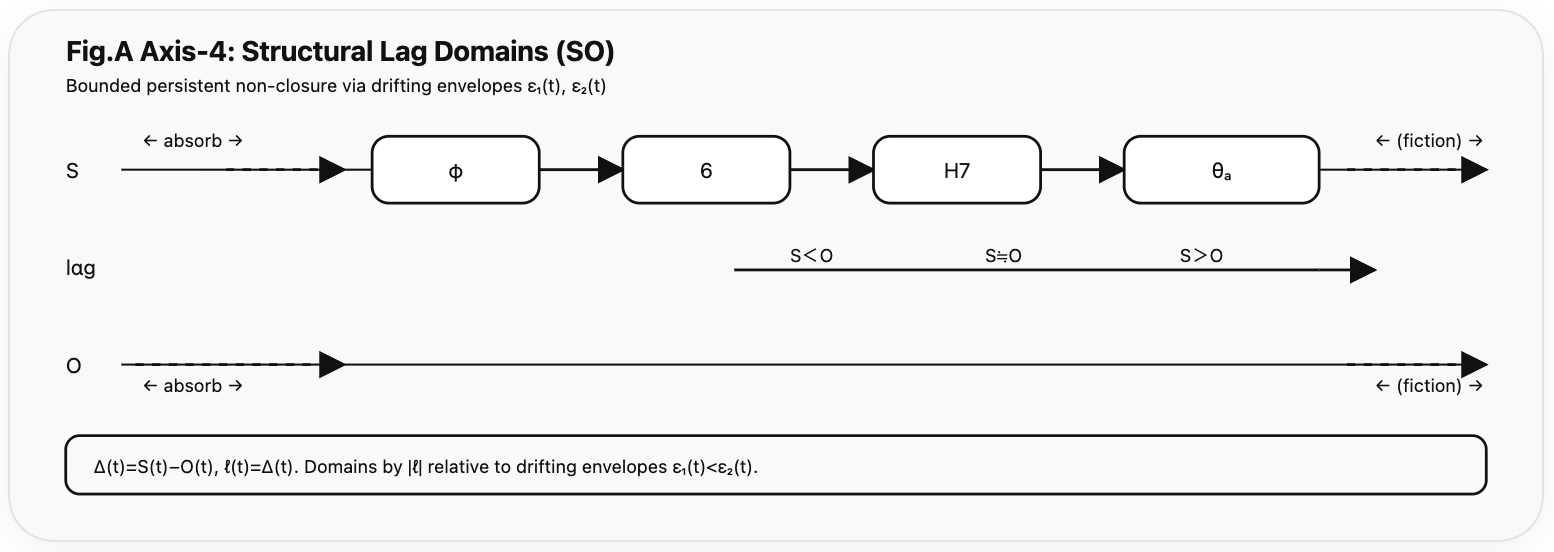
Fig.A:See Fig.B (same remainder, different clock).
The four domains do not represent equilibrium states but bounded regimes under persistent non-closure.
Absorption is intentionally misaligned between $S$ and $O$, encoding non-synchronous entry into structured configurations.
3. Generative Projection
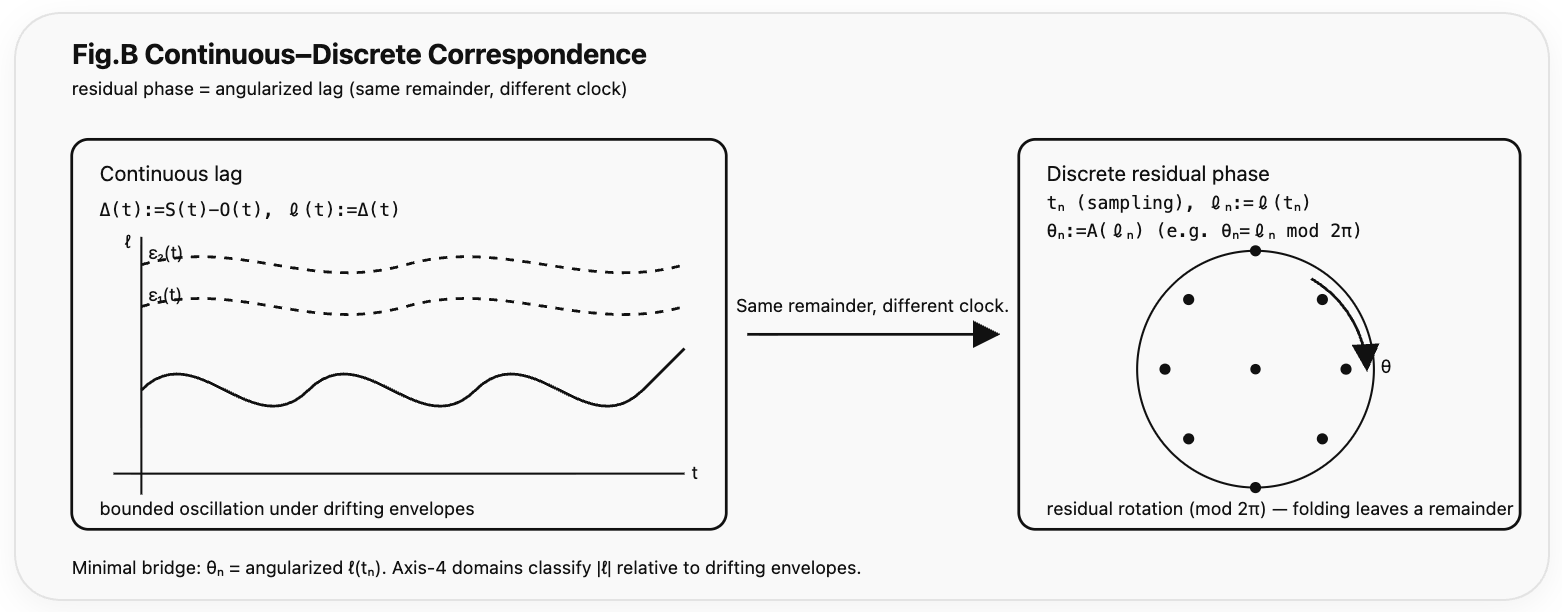
Fig.B:See Fig.A (φ–6–H7–θₐ as lag domains).
Sampling $\ell(t)$ at discrete update times $t_n$ yields
\[\theta_n = \mathcal{A}(\ell(t_n)),\]where residual phase represents the angularized remainder of relational lag.
The continuous remainder and the discrete angular remainder express the same relational surplus under different clocks.
4. Generator Perspective (Minimal Remark)
Discrete update and continuous evolution are classically related by $U = e^{\mathcal A \Delta t}$.
If relational lag is represented by a commutator $\mathcal L = [\mathcal S, \mathcal O]$, then formally $U = e^{\mathcal L}$.
Thus, persistent non-closure may be interpreted as a spectral property of a relational generator.
(See HEG-10 for full spectral discussion.)
5. Consequence
Closure is not required for structure.
Equilibrium is not required for stability.
Axis-4 defines stability as bounded non-convergent persistence and unifies structural classification and generative rotation as two clocks of the same relational remainder.
See HEG-10 for the broader structural context of bounded persistent non-closure.
Fig.A — Structural Axis

Fig.A — Axis-4 Structural Lag Domains (SO configuration).
The relational lag $\ell(t)=S(t)-O(t)$ is classified into four domains ${\phi,6,H7,\theta_a}$ according to its magnitude relative to dynamically drifting envelopes $\epsilon_1(t),\epsilon_2(t)$. Absorption is misaligned between $S$ and $O$.
See Fig.B for the continuous–discrete correspondence (same remainder, different clock).
See also HEG-10 Figure 1 for the broader relational structure of persistent non-closure.
Fig.B — Continuous–Discrete Correspondence

Fig.B — Continuous–Discrete Correspondence of Lag.
The continuous remainder $\ell(t)$ and the discrete residual phase $\theta_n=\mathcal{A}(\ell(t_n))$ represent the same relational remainder under different clocks.
Bounded oscillation under drifting envelopes corresponds to residual rotation modulo $2\pi$.
See Fig.A for the structural classification of SO lag across the $\phi$–$6$–$H7$–$\theta_a$ domains.
This projection relates to HEG-10’s discussion of residual phase and lag classification.
Kernel Note
Axis-4 is a structural compression of HEG-10.
It isolates the minimal relational axis without redeveloping the broader theoretical framework.
#axis-core-prelude #bounded-persistent-non-closure
EgQE — Echo-Genesis Qualia Engine
camp-us.net
© 2025 K.E. Itekki
K.E. Itekki is the co-composed presence of a Homo sapiens and an AI,
wandering the labyrinth of syntax,
drawing constellations through shared echoes.
📬 Reach us at: contact.k.e.itekki@gmail.com
| Drafted Feb 21, 2026 · Web Feb 21, 2026 |