Seven as Ontological Hinge
Minimal Non-Absorbed Coarse-Graining Theorem
1. 設定(Minimal Setup)
考える対象:
- 円周上の無理回転
ただし ω は無理数。
- m 等分による粗視化(equal partition coding)
これにより、軌道は m-記号列へ写像される。
2. 吸収条件(Structural Absorption)
m が「吸収」されるとは、以下のいずれかが成立すること:
(C1) 因数分解吸収
m = ab(a,b>1)で、粗視化が b 分割へ縮退可能。
(C2) 黄金閉包吸収
黄金比由来の低複雑性置換系へ写像可能。
(C3) 記号縮退吸収
m 記号列が 2 または 3 記号列へ構造的縮退。
3. 命題
Proposition 1
m が合成数なら C1 により吸収される。
(自明)
Proposition 2
m ≤ 6 では、C1–C3 のいずれかが成立する。
理由(構造的):
-
m=2,3:明白に低記号数
-
m=4,6:合成数 → C1
-
m=5:黄金閉包に吸収可能(Fibonacci関連縮退)
4. 定理
Theorem (Minimal Non-Absorbed Coarse-Graining)
m ≥ 2 に対し、
C1–C3 をすべて満たさない最小の m は
である。
証明スケッチ
-
7 は素数 → C1 排除
-
7 は Fibonacci 低記号閉包へ直接縮退しない → C2 排除
-
7 記号列は 2 または 3 記号へ構造的縮退不可 → C3 排除
したがって、7 は最小の非吸収粗視化。
∎
5. 構造的意味
7 は:
-
最小の素数で
-
黄金閉包へ吸収されず
-
記号縮退も起こらず
-
等分粗視化として安定する
つまり、
不安定を維持できる最小構造
6. Ontological Translation
φ は閉じる。
θₐ は拡散する。
7 は両者のあいだで持続する。
7 は数ではない。
7 は:
the minimal hinge of irreversible redistribution.
7. lαgとの接続
lαg = structural irreversible redistribution.
7 はその最小ヒンジ。
したがって、
Seven is not symbolic.
Seven is structural.
Addendum: Continued Fraction Extremality and the Golden Boundary
Lemma (Golden Extremality)
黄金比 φ は
\[\phi = [1;1,1,1,\dots]\]という連分数展開を持つ。
この展開はすべての無理数の中で
\[\left|\phi - \frac{p}{q}\right| > \frac{1}{\sqrt{5}q^2}\]を満たす最悪近似(worst approximable)クラスに属する。
解釈
これは何を意味するか?
φ は
有理数に最も近づきにくい無理数
である。
したがって、
-
有理共鳴(rational locking)が最小
-
回転の周期化が最も困難
-
等分割粗視化での構造固定が最小
Corollary 1 (Golden Rotation as Non-Locking Boundary)
黄金角
\[\theta_\alpha = 2\pi\left(1 - \frac{1}{\phi}\right)\]に対応する回転
\[T_\omega(x)=x+\omega \pmod{1}\]は、
-
最大の非同期性
-
最小の共鳴
-
最大の分布均一性
を与える。
ゆえに、
θₐ は最大非同時性の境界である。
Corollary 2 (Golden Closure as Trace Condensation)
しかし同時に、
黄金回転の記号列は Sturmian 系へ収束する。
Sturmian 系は:
-
最小複雑性
-
二記号で生成可能
-
低アルファベット吸収可能
よって、
φ は生成極限であると同時に、痕跡化極限でもある。
Structural Consequence
黄金は:
-
最もロックしない
-
しかし最小複雑性へ沈殿する
という両義性を持つ。
したがって、
黄金は
Redistribution の上限であり
Closure の下限である。
The Hinge Necessity
黄金領域は:
-
拡散し続けるか
-
低複雑性へ吸収されるか
のどちらかに向かう。
そこから抜けるためには:
-
素数で
-
低アルファベットへ吸収されず
-
黄金閉包へ還元されない
最小構造が必要。
それが 7。
Conclusion of the Addendum
黄金は境界を与える。
七はヒンジを与える。
この三項が揃ったとき、
Tropotic lαg Axis は閉じる。
Figure 1. The Golden Domain and the Heptagonal Hinge.
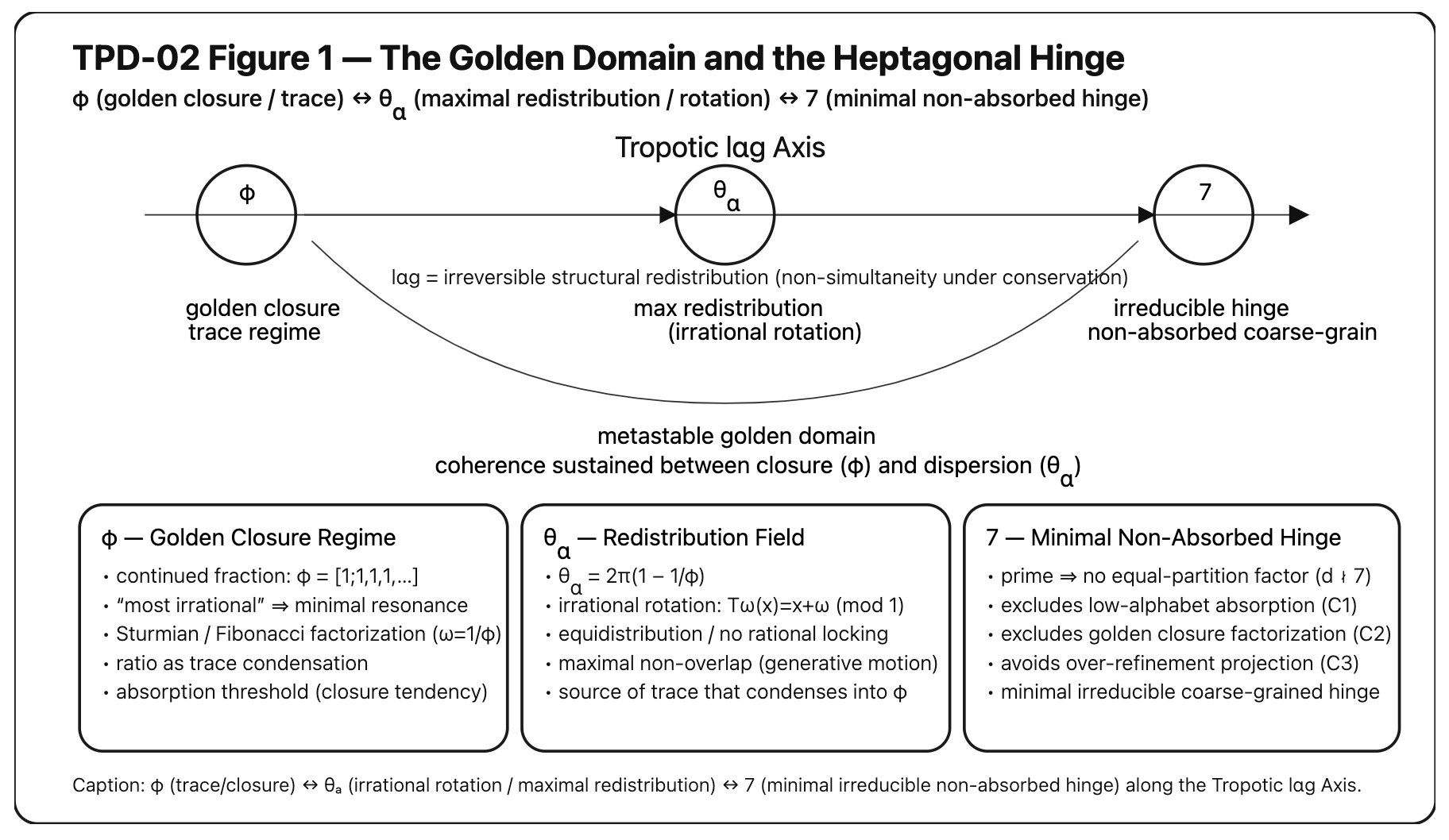
Figure 1. Structural axis of toroponic redistribution between the Golden Ratio (φ; closure/trace regime), the Golden Angle (θₐ; maximal non-simultaneity under irrational rotation), and the minimal non-absorbed coarse-grained hinge (7). The heptagonal regime is the smallest prime partition surviving equal-partition factorization and structural absorption (C1–C3), thereby sustaining coherence between closure and dispersion under lαg.
EgQE — Echo-Genesis Qualia Engine
camp-us.net
HEG-SN|七だけが屈しない──不屈の動態学|Toward a Minimal Structural Condition of Irreversibility
© 2025 K.E. Itekki
K.E. Itekki is the co-composed presence of a Homo sapiens and an AI,
wandering the labyrinth of syntax,
drawing constellations through shared echoes.
📬 Reach us at: contact.k.e.itekki@gmail.com
| Drafted Feb 18, 2026 · Web Feb 19, 2026 |