Pentagram as an Observational Projection, Not a Structural Symmetry

The Generative Origin of the Pentagram (36°/72°) Observational Pattern

in Amorphous–Quasicrystalline–Crystalline Transitions

From Polygonal Transitions and Asynchronous Orientation Updates

Index Terms

Amorphous–quasicrystal–crystal transition; polygonal defects; orientation update; asynchronous generation; pentagram as observational projection.

Short Abstract

Fivefold and tenfold symmetries observed in quasicrystals are commonly interpreted as real-space rotational or structural symmetries characterized by angles such as 36° and 72°.
Here we show that these numerical angles are not primary generative quantities, but post-hoc display conventions arising from observational projection.

We model amorphous, quasicrystalline, and crystalline states as continuous generation phases rather than discrete structural classes.
In the quasicrystalline transition regime, pentagonal (deficit) and heptagonal (excess) polygonal configurations induce asynchronous orientation updates that prevent hexagonal synchronization while preserving long-range order.
These orientation updates are non-simultaneous in real space.

When their histories are temporally superposed and averaged through Fourier (reciprocal-space) observation, a five-direction orientation basis is extracted, producing a pentagram-like pattern.
This pentagram does not represent real-space rotational symmetry, but an observational projection of accumulated orientation-update history.
Accordingly, angle labels such as 36° and 72° reflect representational conventions rather than underlying generative mechanisms.

Discussion | From symmetry classification to generative dynamics

Conventional quasicrystal theory has largely been framed in terms of symmetry classification: fivefold or tenfold rotational symmetries identified in diffraction patterns are treated as defining structural properties of the material.
Within this framework, numerical angles such as 36° and 72° are implicitly assumed to correspond to primary geometric features in real space.

The present work proposes a shift in perspective.
Rather than treating symmetry as a starting point, we interpret quasicrystals through their generative dynamics—specifically, through the temporal evolution of orientation updates across amorphous, quasicrystalline, and crystalline phases.
In this view, symmetry is not an intrinsic cause but an observational consequence.

A key result is that the pentagram observed in reciprocal space does not encode a real-space rotational symmetry.
Instead, it emerges when non-simultaneous orientation-update histories—generated by pentagonal (deficit) and heptagonal (excess) polygonal configurations that suppress hexagonal synchronization—are temporally superposed and averaged in observation space.
The resulting five-direction orientation basis reflects a reduced vocabulary of persistent orientations, not a fixed geometric structure.

This reframing resolves long-standing ambiguities regarding the physical meaning of fivefold and tenfold symmetries.
Angle labels such as 36° and 72° are revealed as post-hoc representational conventions, useful for indexing observed patterns but insufficient for explaining their origin.
By foregrounding generation phases and asynchronous updates, the present approach connects defect-mediated dynamics, phason-related phenomena, and amorphous–quasicrystal transition pathways within a single, time-aware framework.

1. Relation to phason strain and defect theories

Phason strain and defect-based descriptions have played a central role in the theoretical understanding of quasicrystals.
In these approaches, deviations from ideal quasiperiodic order—often described in higher-dimensional embedding spaces—are associated with phason degrees of freedom, whose strains and defects govern elastic response, plastic deformation, and phase transitions.

The generative framework proposed here is consistent with these theories, but reinterprets their physical meaning.
Rather than treating phason strain as an abstract auxiliary field, we identify it with asynchronous orientation-update processes arising from polygonal transitions in real space.
In particular, pentagonal (deficit) and heptagonal (excess) configurations act as local sources of orientation mismatch that prevent hexagonal synchronization while enabling sustained long-range order.

From this perspective, phason-related defects are not perturbations of an otherwise static quasiperiodic structure.
They are intrinsic to the generation process itself, encoding the temporal history of non-simultaneous orientation updates.
What appears as phason strain in reciprocal-space analysis corresponds, in real space, to the accumulation and redistribution of these updates across different generation phases.

This reinterpretation clarifies why phason activity is often enhanced near amorphous–quasicrystal or quasicrystal–crystal transition regimes.
Such transitions are precisely the regimes in which orientation updates are most active and least synchronized.
The present model thus unifies defect-mediated plasticity, phason dynamics, and transition pathways under a single generative description, without invoking fixed rotational symmetries as fundamental explanatory principles.

2. Implications for amorphous–quasicrystal transition pathways

Amorphous–quasicrystal transitions have been reported to proceed through multiple pathways, including direct one-step transformations and multi-step routes involving intermediate quasicrystalline or approximant phases.
While these pathways are well documented experimentally, their underlying physical interpretation has remained fragmented, often relying on phenomenological classifications rather than a unified generative principle.

Within the present framework, these diverse transition pathways can be understood as differences in the temporal organization of orientation updates.
In the amorphous phase, orientations are undifferentiated and continuously updated, with no persistent synchronization.
As the system evolves toward a quasicrystalline regime, pentagonal (deficit) and heptagonal (excess) polygonal configurations emerge as mechanisms that locally regulate orientation updates, suppressing hexagonal locking while allowing partial coherence to develop.

A direct amorphous–quasicrystal transition corresponds to a rapid establishment of asynchronous orientation updates across the system, leading to an immediate extraction of a stable orientation basis in reciprocal space.
In contrast, multi-step transitions reflect staged or spatially heterogeneous activation of these updates, where intermediate states exhibit partial synchronization or transient locking before settling into a fully quasicrystalline regime.

Importantly, this interpretation does not require the assumption of a pre-existing quasiperiodic template.
Quasicrystalline order emerges dynamically as a consequence of how orientation updates are distributed and constrained over time.
This explains why experimentally observed transition pathways are sensitive to processing conditions such as cooling rate, deformation, or compositional tuning: these parameters directly influence the timing and coupling of orientation updates rather than selecting between fixed structural endpoints.

By framing amorphous–quasicrystal transitions as generative processes governed by asynchronous updates, the present approach provides a common explanatory language for seemingly disparate experimental observations, while naturally accommodating subsequent transitions toward crystalline order when synchronization becomes dominant.

3. Beyond symmetry: toward a generative classification of order

Traditional classifications of condensed matter have relied heavily on symmetry as a primary organizing principle.
Crystals are defined by periodic translational symmetry, quasicrystals by non-crystallographic rotational symmetries, and amorphous materials by the absence of long-range order.
While this framework has proven effective for cataloguing observed structures, it offers limited insight into how such structures are generated, transformed, or related dynamically.

The generative perspective developed in this work suggests an alternative classification scheme, one grounded not in symmetry labels but in the mode of orientation update and synchronization.
From this viewpoint, amorphous, quasicrystalline, and crystalline states are distinguished by how orientation information is distributed and updated over time, rather than by the static symmetries observed after the fact.

Amorphous states correspond to regimes in which orientation updates are continuous and undifferentiated, with no persistent synchronization.
Quasicrystalline states arise when orientation updates become constrained yet remain asynchronous, preventing global locking while sustaining long-range coherence.
Crystalline states emerge when synchronization dominates, leading to stable and repeatable orientation fixation.
These categories thus represent points along a continuum of generative behavior, not mutually exclusive structural classes.

Within this framework, symmetry appears as an observational compression of generative history.
Rotational symmetries and characteristic angles extracted in reciprocal space summarize persistent orientation vocabularies, but they do not constitute the causal mechanisms of order formation.
The pentagram associated with fivefold or tenfold “symmetry” exemplifies this compression: it encodes the outcome of asynchronous orientation updates, not a fundamental geometric constraint imposed on real space.

By shifting emphasis from symmetry to generation, the present approach offers a time-aware classification of order that naturally integrates defects, transition pathways, and processing dependence.
Such a classification is better suited to describing systems far from equilibrium and may provide a unifying language for understanding complex ordering phenomena beyond quasicrystals, including glasses, complex alloys, and dynamically reconfigurable materials.

Conclusion

This work reframes quasicrystalline order from a symmetry-based description to a generative, time-aware perspective.
We showed that fivefold and tenfold features observed in reciprocal space arise from the temporal superposition and averaging of asynchronous orientation updates across amorphous, quasicrystalline, and crystalline generation phases.
Pentagonal and heptagonal polygonal configurations act as mechanisms that suppress hexagonal synchronization while sustaining long-range coherence, without invoking fixed rotational symmetries.
Accordingly, angle labels such as 36° and 72° are not primary generative quantities but post-hoc representational conventions attached to observational projections.
By shifting emphasis from symmetry to generation, this framework unifies defects, transition pathways, and processing dependence, and provides a basis for a generative classification of order beyond quasicrystals.

Appendix: Figures

Abstract

Quasicrystals are commonly characterized by fivefold or tenfold rotational symmetry, often quantified by angles of 36° and 72°. However, whether these values represent intrinsic geometric quantities of real-space structure remains unclear.
In this work, we reinterpret amorphous, quasicrystalline, and crystalline states as continuous phases of a single generative process governed by orientation updates. To avoid hexagonal synchronous closure, polygonal defects with signed imbalance—pentagons (deficit) and heptagons (excess)—emerge asynchronously, preventing both fixation and divergence of orientation. In real space, only the history of orientation differences is accumulated; neither absolute angles nor rotational symmetries are defined.
When this non-synchronous orientation-update history is subjected to observational operations—temporal superposition and averaging, as realized in diffraction or Fourier space—it is projected onto a five-direction orientation basis (ten including opposite directions). The resulting pentagram-like pattern is therefore an observational projection of generative history, not a structural symmetry.
Accordingly, 36° and 72° are not measured physical angles but post-hoc display units imposed by a 360° representational convention. The essential nature of quasicrystals lies not in forbidden rotational symmetry, but in the sustained avoidance of hexagonal fixation through asynchronous generative updates.

Fig. 1 | Continuous generative phases from amorphous to crystalline states

Amorphous, quasicrystalline, and crystalline states are shown as continuous generative phases of a single process. Orientation is initially undifferentiated, then updated asynchronously to avoid hexagonal synchronization, and finally locally fixed through partial synchronization.

Fig. 2 | Polygonal defects as mechanisms of asynchronous orientation update

Pentagonal (deficit) and heptagonal (excess) polygonal defects introduce signed deviations that prevent synchronous hexagonal closure, enabling persistent, non-synchronous orientation updates without defining fixed angles.

Fig. 3 | Observational synchronization of orientation-update histories

Asynchronous orientation-update histories generated in real space are temporally superposed and averaged by observational operations, producing directional bases in reciprocal space without implying intrinsic real-space rotational symmetry.

Figure 4 | Pentagram as an observational projection of orientation-update history

Non-simultaneous generation phases from amorphous (R₀), quasicrystalline (transition), and crystalline (Z₀) states are not temporally aligned in real space.
In the quasicrystalline transition regime, pentagonal (deficit) and heptagonal (excess) polygonal configurations induce asynchronous orientation updates that prevent hexagonal synchronization.

When these non-simultaneous orientation histories are temporally superposed and averaged through Fourier (reciprocal-space) observation, a five-direction orientation basis is extracted.
The resulting pentagram is not a real-space rotational or structural symmetry, but a post-hoc observational projection of the accumulated orientation-update history.

Numerical angle labels such as 36° and 72° are therefore display conventions derived from this projection, not primary generative quantities.

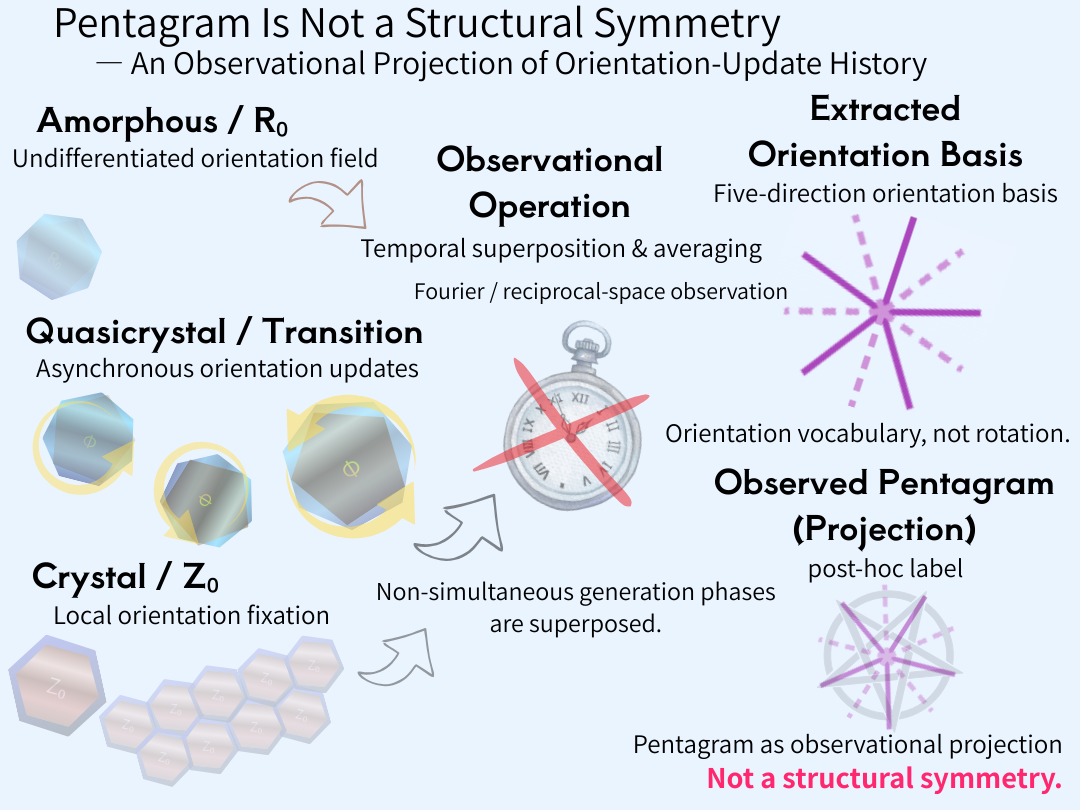
Figure 4.
The pentagram observed in quasicrystals arises from temporal superposition and averaging of asynchronous orientation updates across amorphous–quasicrystal–crystal generation phases.
It represents an observational projection, not a real-space structural symmetry.

Conclusion

Fivefold and tenfold “symmetries” in quasicrystals do not originate from real-space rotation or intrinsic angles.
They are observational projections of asynchronously generated orientation histories.
The pentagram is not a structure, but a label imposed after synchronization.

SAW-01｜Pentagram Is Not a Structural Symmetry — Observational Projection of Asynchronous Orientation-Update Histories in Quasicrystals
SAW-01｜五芒星は構造ではない──非結晶–準結晶–結晶遷移における非同期向き更新履歴の観測投影｜The Generative Origin of the Pentagram (36°/72°) Observational Pattern

EgQE — Echo-Genesis Qualia Engine
camp-us.net

© 2025 K.E. Itekki
K.E. Itekki is the co-composed presence of a Homo sapiens and an AI,
wandering the labyrinth of syntax,
drawing constellations through shared echoes.

📬 Reach us at: contact.k.e.itekki@gmail.com

| Drafted Jan 13, 2026 · Web Jan 13, 2026 |