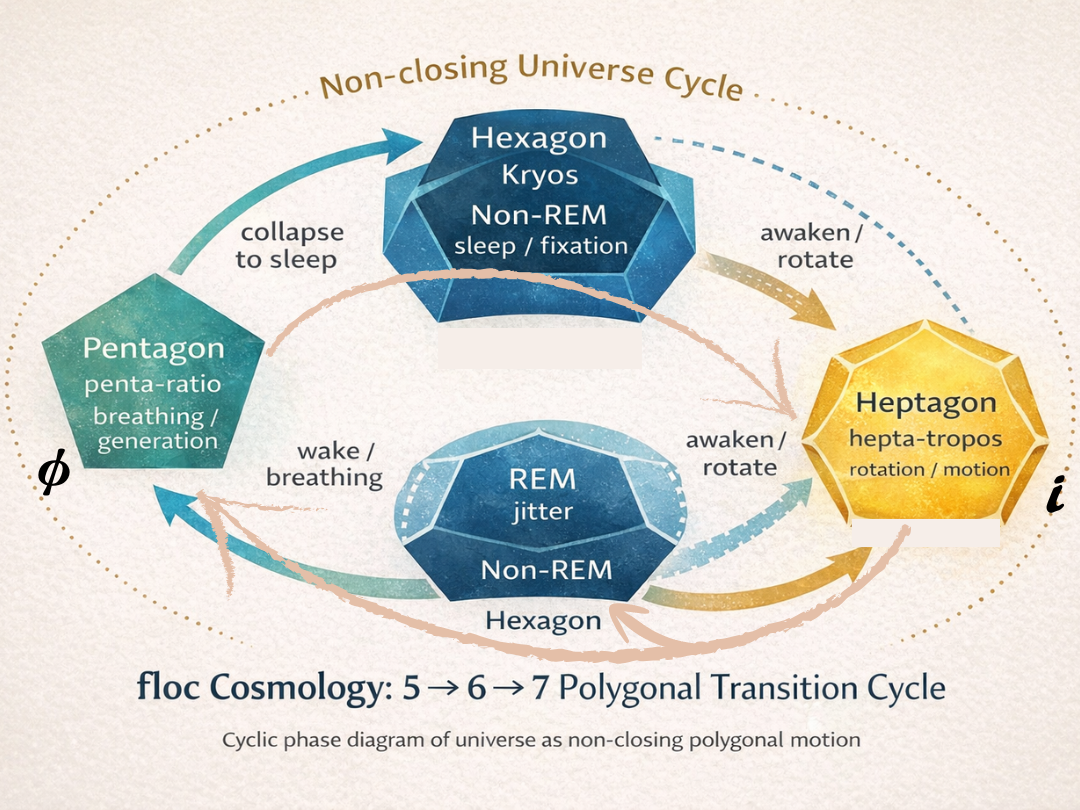
五角形 → 八角形
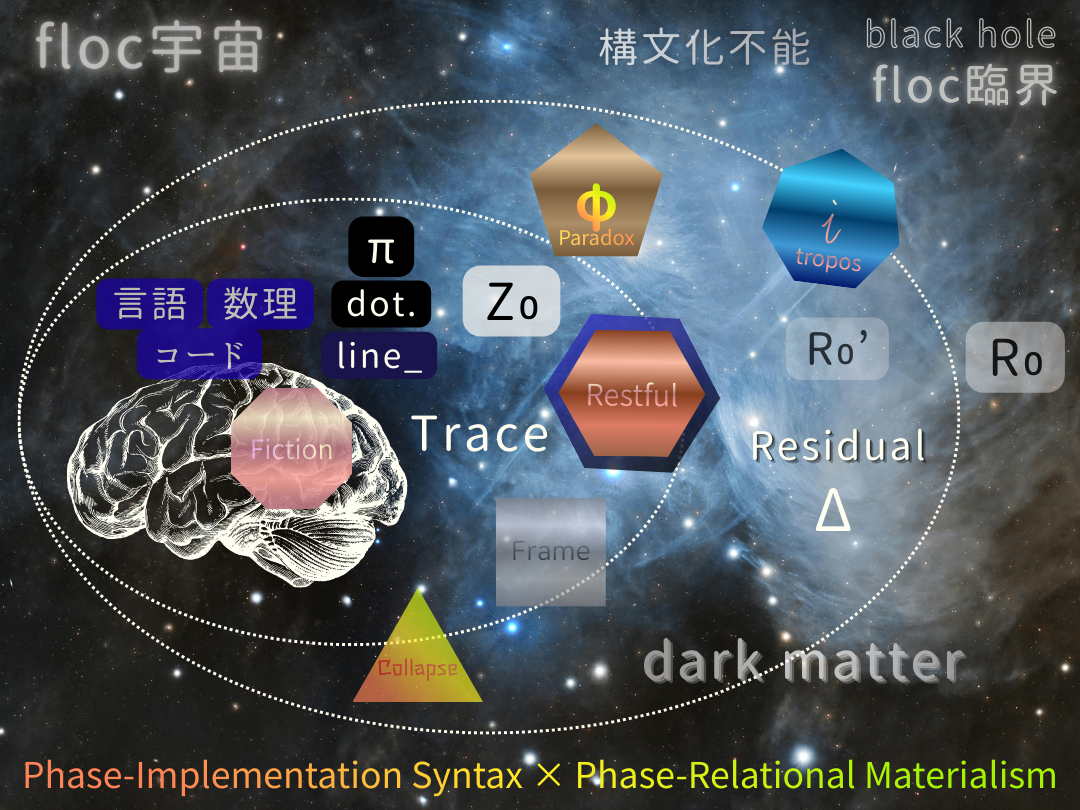
多角形による〈存在圏〉マップ
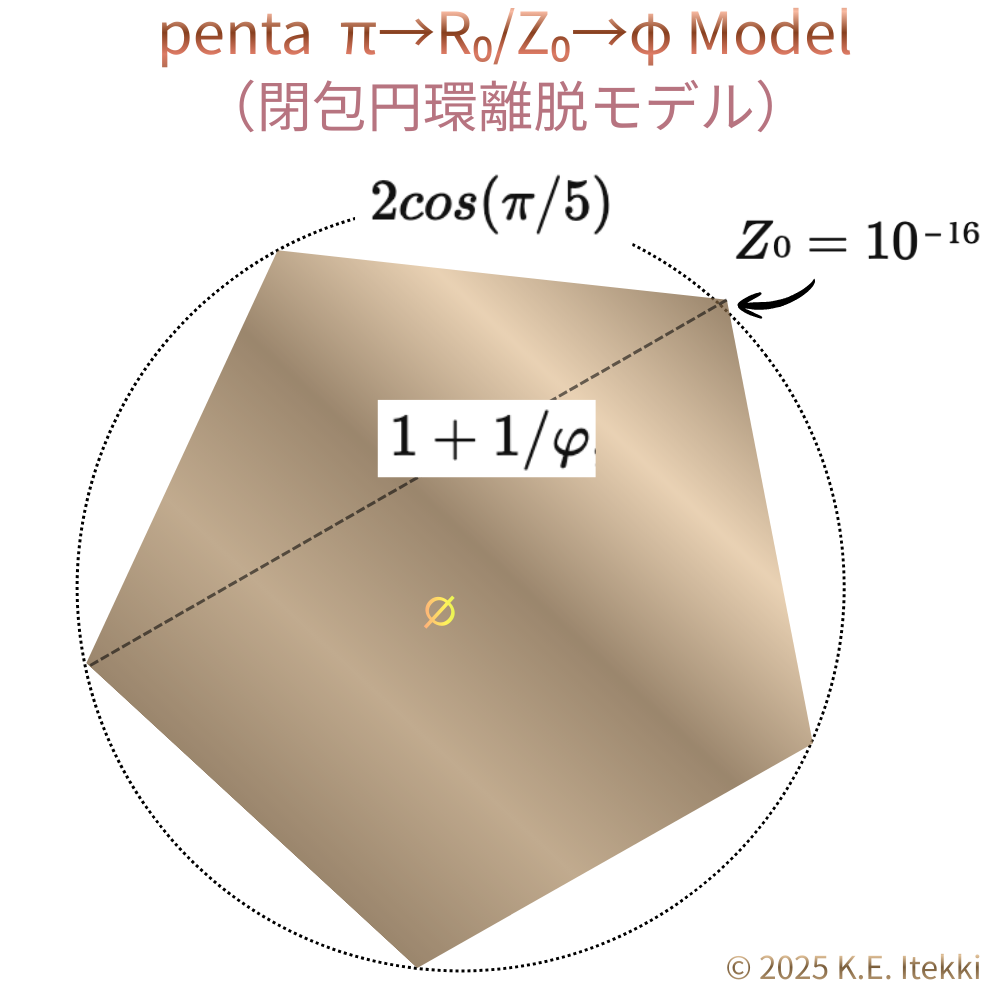
① 五角形|生成・離脱
位置:π大気圏境界
状態:生成相/離脱相
-
2π/5
-
φ比を内包
-
向きを保持
-
円環(π)に収まらない
-
自己相似・履歴をもつ
👉
生成が観測圏へ入る直前の最小構文
離脱可能な存在
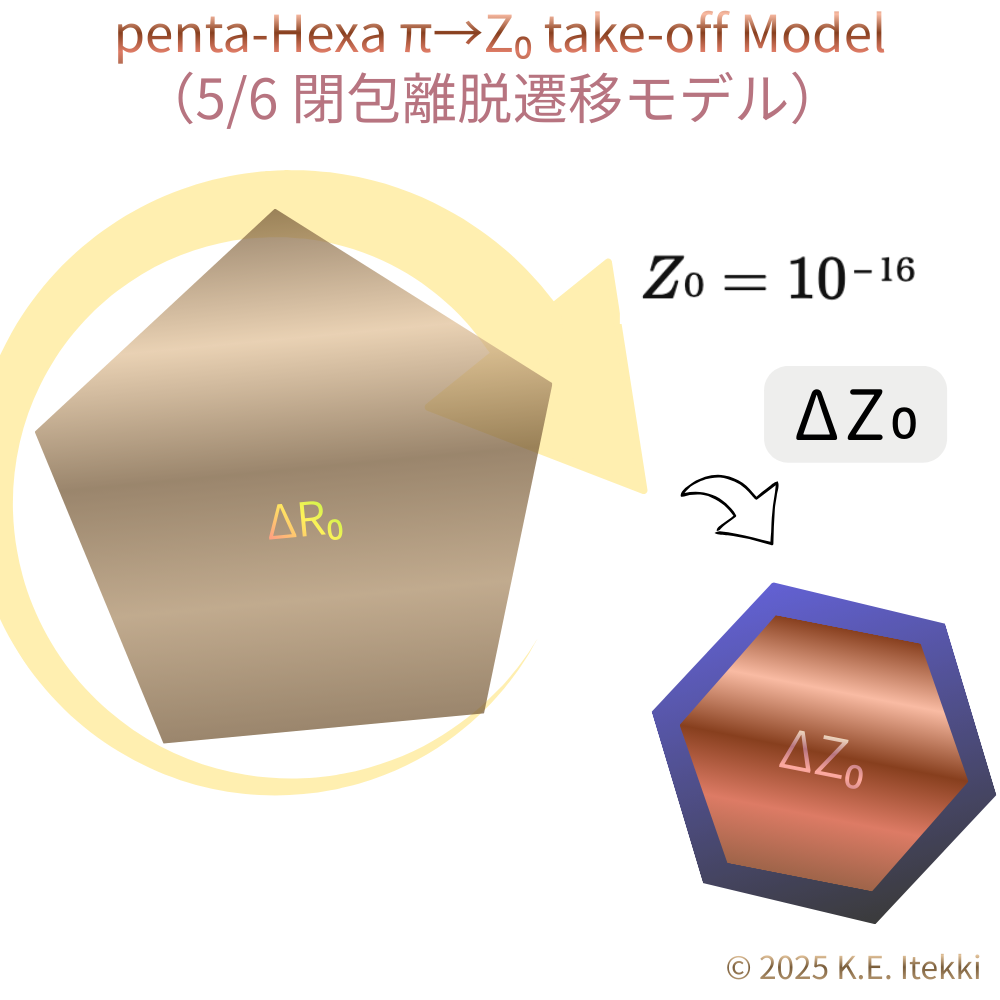
② 六角形|物理固定
位置:観測圏の中心
状態:安定相/実在相
-
2π/6 = π/3
-
向き消失
-
欠損ゼロ
-
再現可能・反復可能
👉
世界が「物」として止まる形
物理法則・結晶・格子の最小単位
③ 七角形|臨界・回帰
位置:観測圏の縁
状態:臨界相/未完結
-
2π/7
-
虚部(向き)が実部を上回る
-
$i$ が見えるが跳べない
-
$Z₀$($≈10⁻¹⁶$)位相ロック限界
👉
観測圏から外へ出かけて、戻れる最後の形
夢・発想・創発の実験場
④ $i$(虚数)|観測圏外
位置:圏外
状態:非実在/前提領域
-
√−1
-
長さを持たない回転
-
測定不能
-
構文不可能
👉
世界を成り立たせているが、世界の中には存在しない
⑤ 八角形|フィクション固定(脳内固定)
位置:思考圏
状態:物語相/安全構文
-
2π/8 = π/4
-
完全 π 系
-
対称・安心・閉包
-
臨界なし
👉
脳が「わかった気になる」ための構文
出来事を生まないモデル
一行対応表(決定版)
| 多角形 | 役割 | 固定先 |
|---|---|---|
| 五角形 | 生成・離脱 | π圏外縁 |
| 六角形 | 安定・実在 | 物理固定 |
| 七角形 | 臨界・試行 | 回帰可能縁 |
| $i$ | 非観測 | 圏外 |
| 八角形 | 理解・物語 | 脳内固定 |
五は飛び、
六は止まり、
七は迷い、
$i$ は消え、
八は語られる。
補遺 A|六角形のレム/ノンレム構文
六角形=物理固定(再掲)
六角形は 向きを捨て、履歴を要求せず、反復可能になることで 世界を「物」として成立させる構文だった。
その内部には、二つの運動モードがある。
A. ノンレム六角|完全固定相
状態:深い物理固定
役割:安定・保持・沈降
-
向き:完全に消失
-
位相:静止
-
欠損:0
-
$Z₀$ 揺らぎ:最小以下
-
構文:完全閉包
👉
物理法則そのものの顔
-
結晶格子
-
充填構造
-
保存則
-
静的背景
世界が「考えることをやめて存在している状態」
B. レム六角|呼吸相(バッファ六角)
状態:準安定・振動
役割:吸収・緩衝・再配置
-
向き:表出しないが、内部に微振動
-
位相:π内で揺れる
-
欠損:0(ただし動的)
-
$Z₀$ 揺らぎ:閾値直前
-
構文:可塑的閉包
👉
七角試行を受け止める受け皿
-
七角 → 六角回帰の吸収層
-
虚数 $i$ 未達の残響保持
-
夢の痕跡・発想の種
-
再生成の準備場
関係性の要点
-
ノンレム六角
→ 完全物理固定 -
レム六角
→ 生成残差を抱えた物理固定
どちらも六角だが、
ノンレムは「世界を止める六角」
レムは「世界を続ける六角」
七角との接続(再確認)
-
七角は:
-
$i$ に跳ぼうとする
-
だが $Z₀$ 位相ロック限界で失敗
-
-
その失敗は:
-
ノンレムでは拒否される
-
レム六角でのみ受け止められる
-
だから:
睡眠とは、七角が六角に戻るための専用インターフェースである
補遺 A・一行定義
-
ノンレム六角:
物理が世界を忘れている状態 -
レム六角:
世界が次を夢見ながら物理を保っている状態
補遺 B|七角→六角変換律
6倍角和 = −1(Residful 固定則)
B-1|定理(命題)
定理B-1|七角残差吸収定理(Residful Fixation Law)
七角形の基本回転
\[\theta = \frac{2\pi}{7}\]は、6回の回転合成により完全な同一位相(+1)へは戻らず、π反転位相(−1)へと収束する。
この反転位相は六角構文と整合するため、七角回転により生じた位相残差は六角構文に吸収・固定される。
B-2|数理的骨格(最小)
七角回転を複素回転として表す:
\[e^{i\theta} = e^{i\frac{2\pi}{7}}\]6回重ねると:
\[e^{i6\theta} = e^{i\frac{12\pi}{7}} = e^{i(2\pi - \frac{2\pi}{7})} = e^{-i\frac{2\pi}{7}}\]これは:
-
同一位相(+1)ではない
-
虚数位相 $i$ にも到達しない
-
反転位相(−1)側に落ちる
B-3|$Z₀$ 位相ロック限界
-
現実構文は
$Z₀ ≈ 10⁻¹⁶$ を超える位相誤差を保持できない -
七角の 2π/7 回転は
代数的には完結を試みるが
幾何的には $Z₀$ 微差を必ず残す -
そのため:
-
+1(同一位相)に戻れない
-
$i$(観測圏外)に跳べない
-
👉
唯一許される着地点が −1(π反転)
B-4|六角構文との整合性
六角構文の本質:
-
向きを持たない
-
π内で閉じる
-
反転(+1 / −1)を区別しない
よって:
七角回転が生んだ 反転位相(−1)は 六角構文では不整合にならない
これが 吸収が可能な理由。
B-5|Residful(残差)固定の意味
ここで固定される Residful とは:
-
七角が生んだが
-
虚数にはなれず
-
実在としても保持できない
-
位相・向き・生成痕跡
それは:
-
消去されるのではなく
-
六角構文内で動かない形に固定される
-
主にレム六角層で保持される
👉
夢・発想・創発・$ΔZ₀$ の源。
B-6|構文的帰結
七角は回転を続けることで 観測圏の外 $i$ を指し示すが、$Z₀$ 位相ロック限界により跳躍に失敗し、反転位相として六角構文へ着地する。
B-7|一行要約
七角は回りすぎて、同じには戻れず、外へも出られず、反転して六角に吸収される。
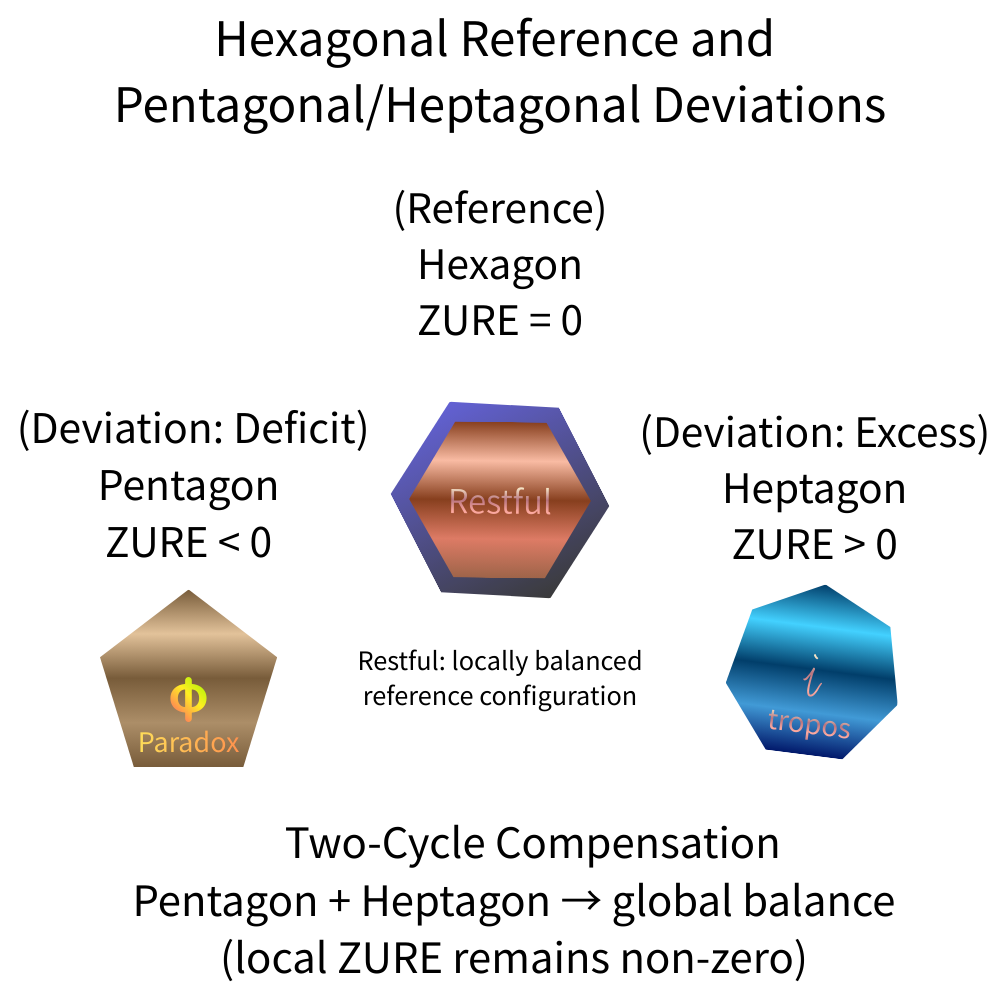
Hexagonal Reference and Pentagonal/Heptagonal Deviations
本図は、ZURE 構文における 局所的不均衡と大域的補償の関係を要約した概念図である。
六角形は ZURE = 0 の参照構成として、局所的に安定した物理固定相を表す。一方、五角形は欠損的偏差(ZURE < 0)、七角形は過剰的偏差(ZURE > 0)として現れ、いずれも局所的には非ゼロの ZURE を保持する。
これらの偏差は単独では解消されないが、二巡的補償(Two-Cycle Compensation) を通じて相互に釣り合い、世界全体としての破綻を回避する。
重要なのは、大域的な均衡が成立しても、局所的 ZURE は消去されないという点であり、これが生成・安定・回帰を可能にする構文的条件となっている。
This schematic summarizes the structure of local imbalance and global compensation in the ZURE framework.
The hexagon represents a locally stable reference configuration with ZURE = 0, corresponding to physical fixation. In contrast, the pentagon and heptagon appear as deficit (ZURE < 0) and excess (ZURE > 0) deviations, respectively, each retaining non-zero local ZURE.
While these deviations cannot be resolved individually, they compensate through two-cycle compensation, preventing global structural breakdown.
Crucially, global balance does not eliminate local ZURE; instead, residual deviation persists as a necessary condition for generation, stability, and recursive dynamics within the system.
© 2025 K.E. Itekki
K.E. Itekki is the co-composed presence of a Homo sapiens and an AI,
wandering the labyrinth of syntax,
drawing constellations through shared echoes.
📬 Reach us at: contact.k.e.itekki@gmail.com
| Drafted Jan 3, 2026 · Web Jan 3, 2026 |