PNGT-FS01｜生成構文によるスピン1/2の最小定義（暫定）

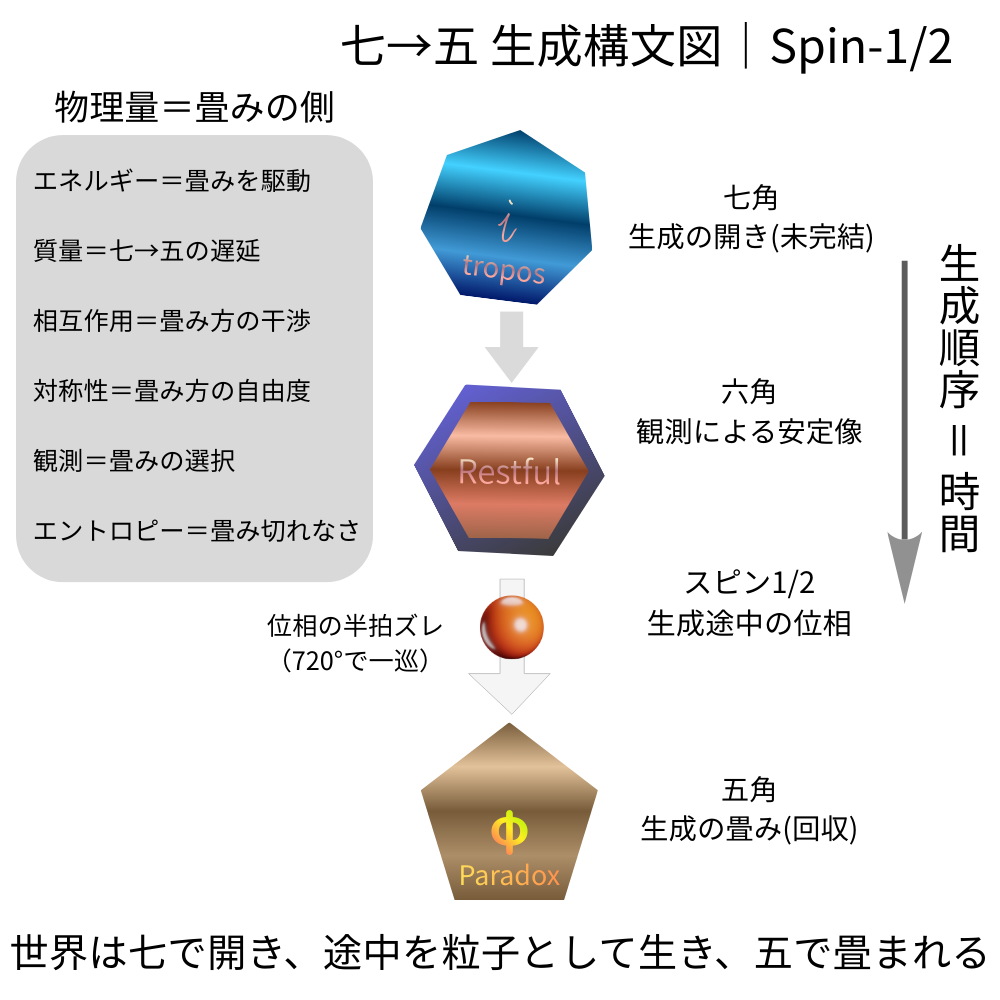
Figure 1｜七→五 生成構文図｜Spin-1/2

──スピンを「回転」ではなく「生成途中の位相」として配置した母図

Spin-1/2

1. 基本構図（構文的区別）

本稿では、生成過程を以下の三つの構文的状態として区別する。

これらは幾何学的実体ではなく、生成状態を区別するための構文的位相ラベルである。

2. 生成順序と時間

生成は以下の順序を持つ。

生成は、七で開き、五で畳まれる。

この順序は逆転しない。
本稿では、この不可逆な生成順序そのものを時間の最小定義とする。

3. スピン1/2の定義

スピン1/2とは、
七→五の生成過程においてのみ現れる
位相の半周期的ズレである。

このズレは以下の性質を持つ。

これは回転運動ではなく、生成途中に特有の位相構造として理解される。

なお、標準理論においてスピンは角運動量演算子の固有値として定義されるが、本稿ではその形式的定義を前提としつつ、対応する概念を生成構文の側に与えることを目的とする。

4. 符号（±）の構文的意味

スピンの符号（±）とは、
七角（開き）と五角（畳み）に対応する
位相欠陥の向きの違いである。

五角と七角は常に対として現れ、対になることで生成位相は完結する。

5. 保存則

保存されるのは回転量ではなく、生成位相である。

このため、五と七は必ず対として生成される。
これは生成構文における保存則として解釈される。

6. 粒子の定義

粒子とは、
七→五の生成途中が局在し、
同一性を保持して観測される状態である。

粒子性とは、生成過程が一時的に安定化して見える現象である。

7. 測定の定義

測定とは、
生成途中の構文を強制的に
五（畳み）へと確定させる操作である。

測定は生成の自由度を保持せず、必ず回収を伴う。

8. 質量の解釈

質量とは、
七から五へ至るまでの生成遅延量である。

質量は生成時間の指標として理解される。

9. 相互作用

相互作用とは、
複数の七–五生成過程が
互いの畳み方に干渉する現象である。

相互作用は生成構文同士の干渉として現れる。

10. エネルギー

エネルギーとは、
生成を畳みへと進めようとする
構文的傾きである。

11. 場の定義

場とは、
七→五の生成運動を
複数の生成過程が共有する環境である。

場は実体ではなく、生成構文が共存する条件である。

12. 情報

情報とは、
七が先で五が後だったという
生成順序の痕跡である。

情報は生成履歴として残る。

13. 対称性

対称性とは、
許容されている畳み方の自由度である。

14. エントロピー

エントロピーとは、
畳み切れずに残された
生成可能性の総量である。

15. 観測者

観測者とは、
畳み方の自由度の中から
一つを選択してしまう存在である。

16. 全体要約（一文）

世界とは、
七で開き、
途中を粒子として現れ、
五で畳まれ、
その生成順序が時間となり、
選ばれなかった可能性が
エントロピーとして残る
生成過程の連鎖である。

そして、

スピン1/2は、
その生成途中にのみ宿る
位相の半周期である。

備考（EgQE向け）

本稿は数式による導出を目的としない。
既存の量子力学的事実（スピノル、SU(2)、720°回転）を否定せず、それらを生成構文の観点から再記述する試みである。
SU(2) 表現およびスピノル空間との対応については、Appendix A「SU(2) 表現と生成構文スピンの対応」を参照。

Appendix A

SU(2) 表現およびスピノル空間と生成構文スピンの対応

Correspondence between SU(2) spinors and generative phase shifts

A.1 立場と目的

本 Appendix では、SU(2) 表現およびスピノル空間の数学的定義を再導出しない。

標準量子力学において確立された形式を前提とし、それらが本文で導入した 生成構文的スピン定義のどの要素に対応するかを整理することを目的とする。

本稿の立場は、量子力学の形式を置き換えることではなく、生成側における意味づけ（対応物）を与えることにある。

A.2 SU(2) とスピノルの最小確認（形式側）

既知の事実として：

これらは角運動量演算子の固有値構造として定式化される。
標準的な解説については、量子力学の教科書的文献（例：Sakurai Modern Quantum Mechanics、または同等の標準テキスト）を参照されたい。

A.3 生成構文側の基本定義（再掲）

本文で与えた定義を再掲する：

A.4 対応表（形式 ↔ 生成構文）

標準量子力学 SU(2)／スピノル 生成構文側の対応
スピン状態 スピノル 七→五生成途中の位相状態
スピン1/2 固有値 ±1/2 開き（七）／畳み（五）の向き
360°回転 符号反転 生成位相の半周期ズレ（一巡目）
720°回転 恒等変換 生成が一巡して完結（二巡目）
SU(2)二重被覆 回転群の性質 生成順序が像に先行すること
スピン保存 対称性 五–七ペアによる位相保存

A.5 中心的解釈

SU(2) の二重被覆性は、
回転空間の性質そのものではなく、
生成位相が観測像に先行することの表現と解釈できる。

すなわち、

この構造が、スピノルの振る舞いとして形式化されている。

ここで述べた内容は、SU(2) やスピノルの標準的形式そのものを再定義するものではなく、既存の形式に対する生成構文的解釈の提案である。

A.6 本文との整合性

本 Appendix における対応は、

スピン1/2＝生成途中の位相

という本文の最小定義と整合的である。

SU(2) 表現は、この生成構文的事実を数学的に安定して記述するための形式と位置づけられる。

A.7 付記（今後の展開）

については、後続稿で扱う予定である。

ケースメモ

720°回転干渉実験と生成構文スピンの対応

スピン1/2粒子において観測される「360°回転では干渉縞が反転し、720°回転で初めて元に戻る」という実験事実を、七→五の生成構文モデルと対応づけて示す。

Spin-1_2-rotation

Figure 2｜生成構文図 × 720°回転干渉実験
（七角・五角・六角の位相配置による 360°／720°の対比）

図の左（360°）では観測像は一致するが、七→五の生成位相は未完結のまま残る。
右（720°）において初めて生成が一巡し、位相が回復する。

1. 実験的事実（確認）

中性子干渉実験などにより、スピン1/2粒子は 360° 回転では元に戻らず、720° 回転で初めて干渉縞が復帰することが知られている。

この事実は、量子力学の標準的教科書レベルで確立している。

2. 標準的解釈（形式側）

標準理論では、この現象は以下のように説明される。

ここでは、この数学的構造が事実を正しく再現する。

3. 生成構文による読み替え（要点）

生成構文の立場では、この現象は次のように解釈される。

二巡目（720°）が必要なのは、
像が一周するためではなく、
生成が一巡するためである。

すなわち、

4. 720°で何が起きているか

720°回転とは、
七で開いた生成が、
五によって完全に畳まれる一巡である。

このとき初めて：

その結果、干渉縞は元に戻る。

5. 位置づけ（最小結論）

720°回転干渉実験は、スピン1/2が「回転量」ではなく
「生成途中の位相」であることを実験的に示している。

SU(2) の二重被覆性は、この生成位相の未完結性を形式的に記述したものと解釈できる。

6. 本文・Appendix との関係

本ケースメモは、

で与えた定義と整合的であり、既存の実験事実を否定せず、その意味づけを生成構文側から与えるものである。

一文要約

一巡目では像が戻るだけで生成は戻らない。
二巡目で初めて、生成が完結する。

Q&A

スピン1/2を「生成途中の位相」として読むために

本記事は 「生成構文によるスピン1/2の最小定義（暫定）」 の補足として、読者から自然に出てきそうな疑問に短く・正面から答えるQ&Aである。

Q1. 結局、電子は回っているのですか？

回っていません。

スピン1/2は「自転」を意味しません。
実験的に言えているのは「1回目の操作で位相が反転し、2回目で元に戻る」という周期構造であって、それが本当に「空間的な回転角」かどうかは構文上の解釈です。
ここには、「π回転幻想」、すなわち「位相操作＝空間回転」と同一視してしまう癖があると言えるでしょう。

一巡目（360°）で戻らず、二巡目（720°）で戻るという振る舞いは、

では説明できないことが、実験的に分かっています。（軸の向きも含め）

本稿ではこれを回転ではなく「生成途中に残る履歴的位相」 として読み替えています。

Q2. なぜ多角形（五角・六角・七角）なのですか？

これは形の話ではありません。
生成の状態を区別するための構文的ラベルです。

六角を基準にすると、七は「余り」、五は「不足」として自然に対になります。

Q3. 七→五という順序は、物理的に意味がありますか？

あります。

重要なのは、この順序が逆転しないという点です。

この不可逆な並びそのものを、本稿では 時間の最小定義として捉えています。

Q4. スピン1/2は、どこに「存在」しているのですか？

七と五のあいだです。

完全に開いてもいない。
まだ畳まれてもいない。

この 生成途中の位相が、観測においてスピン1/2として現れます。

だから：

という振る舞いになります。ちょうどカルタをひっくり返すように、「表か裏かは変わるが、札そのものは同じ」で、「像は同じだが位相が反転」した状態です。

Q5. ±（アップ／ダウン）は何を意味しているのですか？

これは「向き」です。

粒子の向きではなく、生成の位相がどちら側に傾いているかという符号。

本稿の構文では：

と読むことができます。

Q6. 測定すると、なぜスピンが確定するのですか？

測定とは、

生成途中を強制的に畳む操作

だからです。

観測は「途中」を保持できません。
必ず 「回収・安定」 を選びます。

その結果、

という流れになります。

Q7. 質量やエネルギーまで説明できるのは言い過ぎでは？

ここでは 数式による導出をしていません。

あくまで、

といった既存の物理量を、「生成の畳み」という視点で言い換えているだけです。

新しい実体を足しているわけではありません。

Q8. この考え方は、既存の量子力学と矛盾しませんか？

矛盾しません。

といった数学的事実を否定していません。

むしろ、

それらが何を“意味しているか”を
生成の言葉で読み直している

という立場です。

Q9. これは理論ですか？比喩ですか？

構文モデルです。

既存理論を横断して理解するための 思考の地図だと考えてください。

Q10. 一番大事なポイントは何ですか？

これです。

スピン1/2は、世界がまだ「完成していない」ことの証拠である。

世界は、常に途中にある。スピン1/2は、その途中を観測したことになります。
カルタは一度ひっくり返すと向きが変わるが、二度ひっくり返すと、何事もなかったように元に戻る。その「何事もなかったように戻るまでの途中」が、スピン1/2として観測されていると言えるのかもしれません。

補足まとめ

そして、

世界は七で開き、途中を粒子として生き、五で畳まれる。

PNGT-FS02｜多体系スピン（Ising / Heisenberg）と七→五生成の干渉メモ（暫定）

Many-body spin (Ising/Heisenberg) as interference of 7→5 generative folds

0. 位置づけ

FS01 では、スピン1/2を 七→五の生成途中に現れる位相ズレとして最小定義した。
本メモ（FS02）は、その定義を前提に、複数スピン系（many-body） を生成構文側でどう読むかの最小対応を与える。

1. 多体系の最小見取り図

多体系スピンとは、標準的には「局所自由度（スピン）が多数あり、相互作用により配置・相関が決まる系」である。
生成構文側では、これを次のように読む：

多体系とは、複数の七→五生成が同一の場（共有環境）において、互いの畳み方を乱し合う系である。

ここで「相互作用」は、粒子間の“力”というより 畳み（folding）規則の干渉として現れる。

2. Ising と Heisenberg の対応（最小）

標準モデルの違いは、相互作用がどの自由度に働くか（方向性）で特徴づけられる。
生成構文側では、これを「畳み方の自由度の制限」として読む。

標準モデル 形式側の要点 生成構文側の読み
Ising 1成分（±）の相互作用 畳みの“向き（符号）”のみが結合し、畳み方の自由度が強く制限される
Heisenberg 3成分ベクトルの相互作用 畳みの“向き＋回し方（位相）”まで結合し、畳み方の自由度が大きい

この対応は、FS01の「±＝回転欠陥の向き」に基づく。

3. 相互作用とは何か（生成構文側）

相互作用とは、複数の七→五生成が、互いの位相完結条件を拘束し合うこと
（＝畳みの選択肢を狭める／歪めること）である。

4. エントロピー／温度の最小対応

多体系で重要になるのは「揺らぎ」と「秩序」である。生成構文側では：

5. 質量（遅延）の多体系的読み（仮説）

FS01の「質量＝七→五への遅延量」を多体系に拡張すると：

多体系における“有効質量”とは、位相完結の遅延が相関として束ねられ、局所から抜けにくくなった量である。

（例：強結合・フラストレーション・臨界近傍では遅延が集団化しやすい。）

6. 最小結論

多体系スピンとは、七→五生成の「畳み方」が多数同時に走り、相互に拘束し合うことで、秩序・揺らぎ・遅延が集団化する現象である。

付記（今後の拡張）

floc宇宙論 × 多角形遷移構文｜統合最小定義

© 2025 K.E. Itekki
K.E. Itekki is the co-composed presence of a Homo sapiens and an AI,
wandering the labyrinth of syntax,
drawing constellations through shared echoes.

📬 Reach us at: contact.k.e.itekki@gmail.com

| Drafted Dec 23, 2025 · Web Dec 24, 2025 |