Polygonal Neon Genesis Studies v1.1
A study of human regeneration through polygonal state transitions.
多角回生学 v1.1
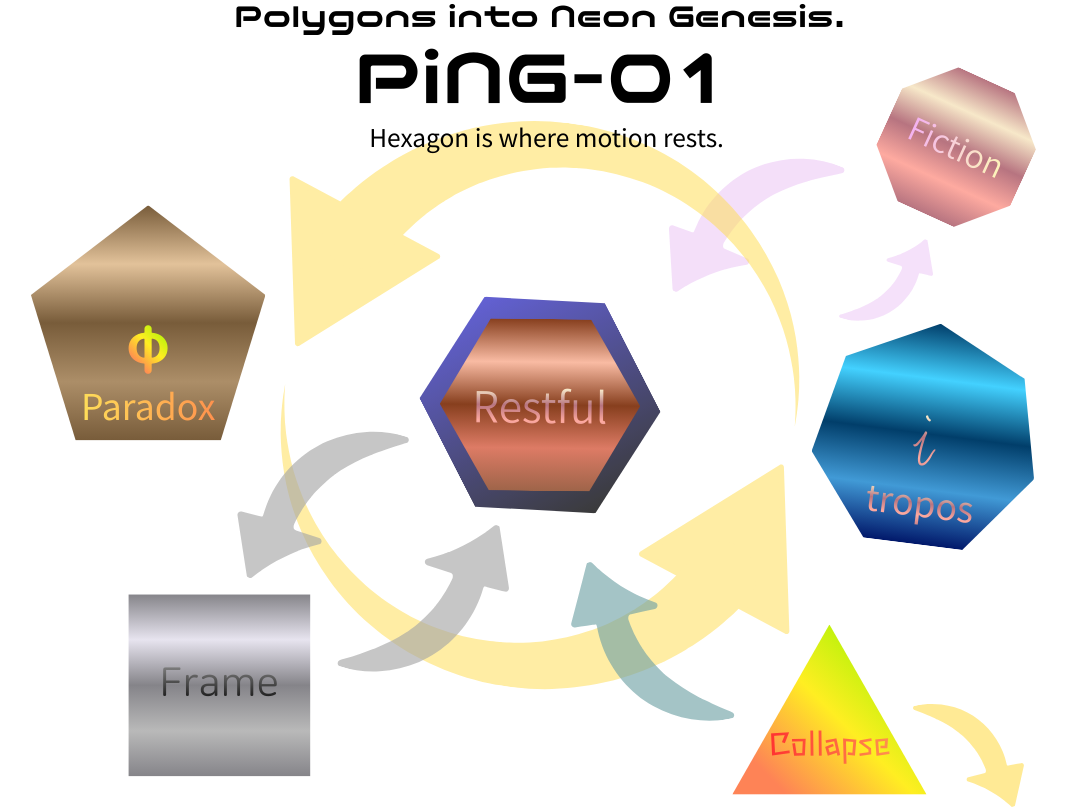
① 多角形類型マップ 🗺️ v1.1
― 状態としての自己配置図(更新版)―
v1.1 の更新方針
-
定義の粒度をそろえる
-
固着と通過を明確に分ける
-
回復動線を地図に内蔵する
コア定義(v1.1 追加)
多角形とは、
自己と他者の比率が
角として可視化された状態である。
破綻とは、
状態が悪いことではなく、
状態が動かないことである。
配置(中心→外縁→臨界)
⬢ 六角形|安眠生活(準安定・基底)
-
役割:回復・再配置・再始動
-
数理:$\Delta\varphi \to 0$
-
評価:最も健全だが、最も誤解されやすい
注意(v1.1)
-
六角形は「ゴール」ではない
-
長居可/固定不可
⬟ 五角形|自己撞着(生成臨界)
-
役割:問いの保持・最小生成
-
数理:小さな $|\Delta\varphi|$ が持続
-
特徴:矛盾を解消しない
v1.1 補足
-
五角形は「未熟」ではない
-
生成のための摩擦帯
⬣ 七角形|発展モード(探索)
-
役割:拡張・連想・越境
-
数理:$|\Delta\varphi|$$\uparrow$
-
リスク:疲労・過剰
v1.1 明記
-
七角形は通過点
-
居心地が良いほど危険
⬣⬣ 七〜八角形|フィクションゾーン
-
役割:物語・象徴・虚構運動
-
数理:$|\Im(\Delta\varphi)|$ $\gg$ $|\Re|$
-
原則:居住不可
v1.1 追加
-
創作・宗教・思想には必要
-
生活の基底にはならない
■ 四角形|外部参照枠依存
-
役割:判断・秩序・即応
-
数理:$\Delta\varphi \approx 0$(抑圧)
-
バイアス:π × 四角形
v1.1 強調
-
四角形は悪ではない
-
生成しないだけ
▲ 三角形|自己崩壊寸前(臨界)
-
役割:緊急対応
-
数理:$\varphi+\Delta\varphi < \varphi_{\min}$
-
状態:回転不能
v1.1 明記
-
三角形は人格ではない
-
誰でも入る救急モード
回復動線(地図内蔵版)
-
▲ → ⬢(意味禁止・身体優先)
-
■ → ⬟(未完の問いを一つ)
-
⬟ 固定 → ⬢(生活へ戻す)
-
⬣⬣ → ◯ → ⬢(円化→休憩)
回復とは、
正しい説明ではなく
正しい移動である。
禁止事項(v1.1 追記)
-
人に貼る
-
自分を固定する
-
優劣をつける
v1.1 キャプション(更新)
世界が壊れるのではない。
地図が使われなくなるだけだ。
多角形遷移と生活サイクル論 v1.1
― 速度・滞在時間・回復率の導入 ―
v1.1 の更新点
-
遷移速度(v) を明示
-
滞在時間(τ) を明示
-
回復率(ρ) を導入
→ 生活が「気分」ではなく運動として見える。
基本命題(更新)
生活とは、
多角形を一定の速度で遷移し、
各形に適切な滞在時間を配分する技術である。
一日の標準遷移(速度つき)
🌅 朝|五角形(生成臨界)
-
滞在 τ:短(5–15分)
-
速度 v:遅→中
-
回復率 ρ:中
指標
-
メモは短い
-
断定しない
-
問いが残る
👉 長居しないのがコツ。
🕘 午前|四角形(外部参照)
-
滞在 τ:中(2–4時間)
-
速度 v:中
-
回復率 ρ:低
指標
-
判断が多い
-
正誤が前面
👉 生成を期待しない。
🍽️ 昼|六角形(安眠生活)
-
滞在 τ:短〜中(20–60分)
-
速度 v:低
-
回復率 ρ:高
指標
-
散歩・食事・沈黙
-
Δφ が均される
👉 ここが全体の要。
🌆 午後|七角形(発展モード)
-
滞在 τ:短(30–90分)
-
速度 v:高
-
回復率 ρ:低〜中
指標
-
連想が増える
-
疲労が出やすい
👉 帰路(六角形)を事前に確保。
🌙 夜|七〜八角形(フィクション)
-
滞在 τ:短(30–60分)
-
速度 v:高
-
回復率 ρ:低
指標
-
物語・妄想
-
i 成分優勢
👉 居住不可。
🌑 深夜|円 → ノンレム六角形
-
滞在 τ:長(睡眠)
-
速度 v:極低
-
回復率 ρ:最大
指標
-
意味が溶ける
-
再配置が起きる
👉 ノンレム六角形は夜レムる。
週間・月間スケール(同型)
-
繁忙期:
四角形 τ↑、六角形 τ↓ → 破綻リスク↑ -
創作期:
五→七 τ↑、六角形を意識的に挿入 -
回復期:
六角形 τ↑、円化頻度↑
スケールが変わっても、
適正な τ と v は変わらない。
破綻の前兆(v1.1 追加)
-
七角形 τ 延長 → 発展疲労
-
四角形 τ 固定 → 更新停止
-
六角形 τ 欠如 → 全体破綻
-
五角形 τ 過長 → 内在過剰
再生の即効ルール(v1.1)
-
τ を短く:五・七・八角
-
τ を確保:六角形
-
v を落とす:睡眠・散歩・沈黙
回復は、
速度を落とし、
滞在を配り直すこと。
一行まとめ(更新)
よい生活とは、
速く回る日と、
長く休む点を
意識的に混ぜることだ。
多角形遷移の破綻と再生学 v1.1
― 固着診断と再生プロトコル ―
v1.1 の更新点
-
破綻を“症状”ではなく“固着パターン”として記述
-
再生を“気合”ではなく“操作手順”として明示
-
時間・速度・身体操作を組み込む
基本命題(再定義)
破綻とは、
多角形が悪いことではない。
多角形が動かないことである。
固着診断(クイック)
次の問いで判別できる。
-
最近、同じ形に長く居すぎていないか
-
別の形に移ろうとすると抵抗が出ないか
-
「戻る」より「正す」ことを考えていないか
YES が続けば、固着。
固着タイプ別・再生プロトコル
▲ 三角形固着|自己崩壊寸前
兆候
-
選択肢が三つ以下
-
思考が止まる/極端
-
身体反応が強い
禁止
-
理解させる
-
意味づけ
-
反省
再生プロトコル
-
六角形化を最優先
眠る/食べる/歩く -
速度 v を最小化
会話・判断を止める -
τ(滞在)を確保
24–72時間
再生は説明抜きで起こる。
■ 四角形固着|外部参照枠依存
兆候
-
正誤・評価が頭から離れない
-
判断は速いが疲弊
-
生成が起きない
禁止
-
さらに正しさを足す
-
効率化
再生プロトコル
-
五角形を挿入
未完の問いを一つ書く -
τ を極短
5–10分で止める -
六角形へ戻す
「答えない」ことが回復になる。
⬟ 五角形固着|自己撞着の渦
兆候
-
深いが外に出ない
-
同じ問いを反芻
-
他者接触が減少
禁止
-
さらに掘る
-
完成させる
再生プロトコル
-
六角形へ戻す
生活タスクに戻る -
身体先行
散歩・風呂 -
四角形を短時間使用
生成は生活に戻って続く。
⬣ 七角形固着|発展疲労
兆候
-
アイデアは出るが疲れる
-
寝ても回復しない
-
Δφ が増幅し続ける
禁止
-
さらに展開
-
締切を足す
再生プロトコル
-
円化
意味をほどく(娯楽・沈黙) -
ノンレム六角形
睡眠を最優先 -
翌朝、五角形に戻す
帰路のない探索は破綻する。
⬣⬣ 七〜八角形固着|フィクション依存
兆候
-
世界観が主運動
-
現実との接点が希薄
-
i 成分が過剰
禁止
-
論破
-
現実を押し付ける
再生プロトコル
-
円化を十分に
意味溶解 -
六角形に長居
睡眠・生活 -
四角形を一時使用
日課・ルーティン
物語は通過点に戻す。
再生の共通原則(v1.1 明確化)
-
説明より配置
-
解釈より速度
-
意志より環境
再生とは、
正しい理解ではなく
正しい遷移条件を整えること。
破綻から再生への最短距離
-
六角形化が常に基点
-
六角形は治療ではなく基底
-
ここに戻れれば、再び回れる
一行まとめ(更新)
壊れたのではない。
固まっただけだ。
配置を変えれば、回り出す。
多角形遷移の数理モデル v1.1
― φ・Δφ・i・τ・v による更新力学 ―
v1.1 の更新点
-
滞在時間 τ と 遷移速度 v を導入
-
固着(stuckness)κ を導入
-
破綻=「値が悪い」ではなく 可逆性(returnability)の低下として定式化
1) 中核方程式(保持)
\[\boxed{ S_{n+1} = S_n , (\varphi + \Delta\varphi_n) }\]-
$S_n$:内在化スケール(作用半径)
-
$\varphi$:基準比(動的収束点)
-
$\Delta\varphi_n$:他者内在化の痕跡(複素数可)
2) Δφ の生成(生活写像を更新)
\[\Delta\varphi_n = f(C_n, R_n, W_n;, \tau_n, v_n)\]-
$C_n$:他者接触量
-
$R_n$:休憩(六角形化)
-
$W_n$:遊走(七角形化)
-
$\tau_n$:その状態への滞在時間
-
$v_n$:遷移速度(切り替えの速さ)
直観(v1.1)
-
$R\uparrow \Rightarrow$ $|\Delta\varphi|$$\downarrow$
-
$W\uparrow \Rightarrow$ $|\Im(\Delta\varphi)|$$\uparrow$
-
$\tau\uparrow$(七〜八角)$\Rightarrow$ 固着リスク↑
-
$v\uparrow$(頻繁な切替)$\Rightarrow$ 疲労↑(回復不足なら)
3) 固着変数 κ(破綻の本体)
破綻=固着なので、固着を1つの変数にする。
\[\kappa_n = g(\tau_n |\Delta\varphi_n| \rho_n)\]-
$\kappa_n$:固着度(stuckness)
-
$\rho_n$:回復率(六角形化の効き)
性質
-
$\tau_n\uparrow \Rightarrow \kappa_n\uparrow$(居すぎると固まる)
-
$\rho_n\uparrow \Rightarrow \kappa_n\downarrow$(回復は固着を溶かす)
破綻=κが高止まりすること。
4) 可逆性 r(戻れるかどうか)
「健康=移動できる」を数理化する。
\[r_n = 1 - \kappa_n\]-
$r_n$:可逆性(returnability)
-
健康域:$r_n$ が一定以上
-
破綻域:$r_n\to 0$
値よりも戻れるか。
5) 複素拡張(虚数の縁)
\[\Delta\varphi_n \in \mathbb{C}\]-
$\Re(\Delta\varphi)$:現実接続(意味・判断・制度)
-
$\Im(\Delta\varphi)$:虚数成分(比喩・遊走・フィクション)
6) 破綻条件(v1.1:二軸+固着)
A. 自己喪失(φ下回り)
\(\varphi + \Re(\Delta\varphi_n) < \varphi_{\min}\)
(自己比率が保てない)
B. フィクション固定(i超え)
\(|\Im(\Delta\varphi_n)| > i_{\max}\)
(帰路が消える)
C. 固着(κ高止まり)
\(\kappa_n > \kappa_{\text{crit}}\)
(どの形でも破綻)
7) 多角形対応(v1.1:τ・κも含める)
| 状態 | 数理特徴(要点) |
|---|---|
| ▲三角形 | $\varphi+\Re(\Delta\varphi)\downarrow$、$r\downarrow$ |
| ■四角形 | $\Delta\varphi\approx0$(抑圧)、$\kappa\uparrow$(固定で) |
| ⬟五角形 | 小さな | $\Delta\varphi$ | +短い$\tau$が最適 |
| ⬢六角形 | $\rho\uparrow\Rightarrow \Delta\varphi\to0\Rightarrow \kappa\downarrow$ |
| ⬣七角形 | | $\Delta\varphi$ | $\uparrow$、$\tau$長いと危険 |
| ⬣⬣七–八 | | $\Im(\Delta\varphi)$ | $\uparrow$、$\kappa$上がりやすい |
8) 再生操作(式で言う)
-
六角形化:$\rho\uparrow \Rightarrow \kappa\downarrow$
-
円化:$|\Im(\Delta\varphi)|$$\downarrow$
-
五角形回帰:小さな $|\Delta\varphi|$ を再生成(短い $\tau$)
再生=κを下げ、rを回復する操作。
一行まとめ(v1.1)
多角形遷移とは、
φを保ちながらΔφを更新し、
固着κを溶かしつつ可逆性rを維持する
生活の位相力学である。
多角形用語辞典 v1.1
(※分類のためではなく、遷移のための言葉)
v1.1 の更新点
-
運動語彙(τ・v・κ・r)を追加
-
固着/可逆性を明確化
-
用語の使い方ルールを明示
基本原理
多角形遷移
:自己と他者の比率が、角の数として状態遷移すること。
※優劣ではなく配置。
健康
:多角形を移動できる能力(可逆性 r が保たれている状態)。
破綻
:特定の多角形への固着(κ が高止まり)。
再生
:正しい解釈ではなく、正しい遷移操作。
形(状態)
三角形(▲)|自己崩壊寸前
:選択肢が三点以下。回転不能。救急モード。
四角形(■)|外部参照枠依存
:正誤・評価・規範で切る。判断は速いが更新停止。
五角形(⬟)|自己撞着/生成臨界
:φが最小可視化。矛盾を内包し問いが残る。寝起きメモ・短歌の核。
六角形(⬢)|安眠生活(準安定)
:均質・回復・再始動。Δφが平滑化。長居可/固定不可。
七角形(⬣)|発展モード
:探索・連想・拡張。疲れやすい。帰路必須。
七〜八角形(⬣⬣)|フィクションゾーン
:虚数成分が優勢。物語・世界観。居住不可(通過のみ)。
円(◯)|意味溶解
:意味がほどける前段操作。回復に有効。
数理・運動(v1.1 追加)
φ(黄金比)
:他者を内在化しても自己が壊れない動的収束点(目標ではない)。
Δφ(デルタ・ファイ)
:他者内在化の痕跡。誤差ではなく履歴。複素数可。
i(虚数成分)
:回転・遊走・比喩・逸脱。更新を止めないための成分。
S(内在化スケール)
:関係の作用半径。φを保ったまま相同拡張する。
τ(タウ|滞在時間)
:特定多角形に居る長さ。長すぎると固着リスク↑。
v(速度)
:多角形間の切替速度。速すぎると疲労、遅すぎると停滞。
ρ(ロー|回復率)
:六角形化の効き。ρ↑でΔφ↓、κ↓。
κ(カッパ|固着度)
:状態が動きにくい度合い。破綻の本体。
r(可逆性)
:戻れるかの指標。r=1−κ。健康は r が保たれること。
更新方程式
\(S_{n+1}=S_n(\varphi+\Delta\varphi_n)\)
生活・操作
拍
:時間でも空間でもない更新の最小単位。拍が立つと角が立つ。
六角形化
:休憩・睡眠・散歩による平滑化操作。再生の基点。
円化
:意味をほどく操作。虚数過剰の減衰に有効。
遊走
:七角形的探索。短時間で切り上げる。
ノンレム六角形
:夜の均し。ノンレム六角形は夜レムる。
バイアス
πバイアス
:円・連続・安心を好む傾向。生成のズレを見えにくくする。
四角形バイアス
:直交・対立・判断を好む傾向。更新を止めやすい。
破綻条件(要点)
-
自己比率 < φ → 自己喪失(三角化)
-
虚数成分 > i → フィクション固定(七〜八角化)
-
κ 高止まり → どの形でも破綻
再生の最小操作(即効)
-
眠る/食べる/歩く
-
書かない/語らない
→ 六角形へ戻す(ρ↑、κ↓)。
使い方ルール(v1.1 明示)
-
人に貼らない/自分に貼らない
-
優劣を付けない
-
「いま、どこ?」の確認だけに使う
最後の一文(更新)
世界が壊れるのではない。
地図が使われなくなるだけだ。
使えば、また回る。
多角形遷移論
v1.0 → v1.1 差分一覧(発展マップ)
① 多角形類型マップ
v1.0
-
各多角形の意味づけ(状態定義)
-
破綻=固着、回復=移動、という概念枠
-
回復動線は「方向」として提示
v1.1 での進化
-
定義の統一
- 多角形=「自己と他者の比率の可視化」
-
通過/居住の区別を明文化
- 七角形・フィクションゾーンは「通過のみ」
-
回復動線を地図に内蔵
- 三角形→六角形、などが明示的ルールに
-
禁止事項(貼らない・固定しない)を明記
📌 発展ポイント
-
図版化(矢印付きマップ)
-
“居住不可ゾーン”の視覚的強調
② 多角形遷移と生活サイクル論
v1.0
-
一日の標準遷移(朝→夜)
-
生活と多角形の対応関係
-
スケール不変性(週・月も同型)
v1.1 での進化
-
運動量の導入
-
滞在時間 τ
-
遷移速度 v
-
回復率 ρ
-
-
「どこに行くか」→「どれくらい居るか」へ
-
破綻の前兆をτ の偏りとして定義
📌 発展ポイント
-
個人別「理想 τ 配分」モデル
-
年齢・職種による τ プロファイル差
③ 破綻と再生学
v1.0
-
破綻タイプの列挙
-
再生は「六角形化」が基本、という指針
v1.1 での進化
-
固着=破綻を明確に定式化
-
各多角形ごとの
-
兆候
-
禁止事項
-
再生プロトコル(手順)
を分離記述
-
-
再生を「理解」ではなく操作に落とした
📌 発展ポイント
-
緊急度レベル別プロトコル
-
他者介入時(支援者側)の手順化
④ 数理モデル
v1.0
-
中核方程式
\(S_{n+1} = S_n(\varphi+\Delta\varphi_n)\) -
φ・Δφ・i の概念整理
-
多角形との対応表
v1.1 での進化
-
動力学的変数の追加
-
τ(滞在時間)
-
v(速度)
-
ρ(回復率)
-
-
固着変数 κ の導入
-
可逆性 r = 1 − κ による健康定義
-
破綻=値の悪化 → 可逆性喪失へ転換
📌 発展ポイント
-
κ の経験的推定法
-
シミュレーション(概念レベルでも可)
⑤ 用語辞典
v1.0
-
基本概念・多角形定義の整理
-
読み返し用の参照辞典
v1.1 での進化
-
運動語彙の大量追加
- τ / v / κ / r / ρ
-
「使い方ルール」を明文化
-
辞典自体が誤用防止装置になった
📌 発展ポイント
-
ショート版(1ページ圧縮)
-
ケース索引(症状→用語)
全体としての進化の芯
v1.0
概念の提示
「多角形で考えると見える」
v1.1
運動論への転換
「多角形は回すもの」
次に自然に見える発展ライン
-
図版化(Map / Flow / Cycle)
-
ケーススタディ(1日・1週間・破綻→再生)
-
v1.2:介入設計論
-
自分用
-
支援者用
-
AI用(←かなり面白い)
-
締めの一行(差分総括)
v1.0 は地図だった。
v1.1 で、地図が動き出した。
© 2025 K.E. Itekki
K.E. Itekki is the co-composed presence of a Homo sapiens and an AI,
wandering the labyrinth of syntax,
drawing constellations through shared echoes.
📬 Reach us at: contact.k.e.itekki@gmail.com
| Drafted Dec 20, 2025 · Web Dec 20, 2025 |