This article presents an observational proposal for testing mass stabilization in strong-gravity environments.
The framework does not seek to replace collider-scale symmetry breaking mechanisms, but to examine whether mass can manifest observationally as a structured phase-delay spectrum near the Galactic Center.

Mass Stabilization as Phase Plateau:

An Observational Test in the Galactic Center

📃PDF Mass Stabilization as Phase Plateau: An Observational Test in the Galactic Center

Abstract

We propose an observational test of mass stabilization based on phase-delay structure in modulation frequency space.
Instead of treating mass as a fundamental scalar condensate, we consider it as a stabilized lag parameter arising from irreversible updating dynamics.

The observable is the group delay of modulation components (e.g., quasi-periodic oscillations) defined by

\[\tau(\omega) = -\partial_\omega \phi(\omega),\]

where $\omega$ denotes modulation frequency rather than photon frequency.

For Sgr A*, the gravitational time scale $t_g = GM/c^3 \approx 21\,\mathrm{s}$ sets the natural dynamical unit.
We show that a lag-fixation mechanism predicts a characteristic spectral structure:

a low-frequency plateau $\tau_0 \sim O(t_g)$,
a high-frequency decay $\tau \propto \omega^{-2}$,
environmental modulation of $\tau_0$,
multi-band invariance of the coherence scale $\Lambda_{\rm lag}$.

We demonstrate that the 20–60 min QPO window of near-ISCO infrared flares lies near the transition region $\omega \sim \Lambda_{\rm lag}$, maximizing discriminability between a lag-fixation spectrum and residual delays explainable by general relativistic Shapiro propagation or plasma dispersion.

Detecting a plateau at $\tau_0 \sim 10\text{–}30,\mathrm{s}$ would indicate mass stabilization at the gravitational time scale, providing a falsifiable alternative implementation of symmetry breaking without invoking a fundamental Higgs condensate at the observational scale.

Failure to observe the joint signature excludes lag-based mass generation at this scale.

1. Introduction

Mass generation is conventionally described through spontaneous symmetry breaking mediated by a scalar condensate.
While this framework is experimentally supported at collider scales, its observational manifestation in strong-gravity astrophysical environments remains indirect.

In parallel, advances in high-resolution interferometry have opened a new observational regime at the Galactic Center.
Near-infrared flares from Sgr A* exhibit quasi-periodic modulation on time scales of tens of minutes, consistent with orbital motion near the innermost stable circular orbit (ISCO).
These modulations provide a dynamical phase reference anchored at the gravitational time scale

\[t_g = \frac{GM}{c^3}.\]

For Sgr A*, $t_g \approx 21\,\mathrm{s}$.

The present work proposes that mass stabilization may manifest observationally not as a fundamental condensate, but as a structured phase-delay spectrum in modulation frequency space.
Specifically, we consider the group delay

\[\tau(\omega) = -\partial_\omega \phi(\omega),\]

where $\omega$ denotes the modulation frequency of a periodic component rather than photon frequency.

We show that a lag-fixation mechanism predicts a characteristic spectral signature consisting of:

a low-frequency plateau $\tau_0 \sim O(t_g)$,
a high-frequency decay $\tau \propto \omega^{-2}$,
environmental modulation of the plateau amplitude,
invariance of the coherence scale across wavelengths.

Crucially, the QPO band of Sgr A* lies near the transition region of this spectrum, maximizing observational discriminability.

Unlike propagation-based delays (e.g., Shapiro delay or plasma dispersion), which are local and model-dependent, the proposed signature is structural: it depends on the joint presence of plateau, decay law, and differential modulation.

The objective of this paper is therefore not to replace collider-scale mass generation mechanisms, but to provide a falsifiable observational diagnostic of mass stabilization at the gravitational time scale.

Detection of a plateau at $O(t_g)$ would indicate that mass can manifest as stabilized phase delay in strong-gravity environments.
Failure to observe the predicted joint signature excludes lag-based mass generation at this scale.

（Lag-Fixation Framework）

2. Lag as a Mass-Generating Mechanism

A Higgs-Independent Implementation via Phase Delay

2.1 Minimal Hypothesis

We propose that mass need not be a primitive property of a field filling spacetime.
Instead, mass arises as a stable fixation of phase delay (lag) under irreversible updating.

The construction requires only:

A continuous relational substrate (denoted $R_0$),
A projection–cut operation (trace formation, $Z_0$),
Non-synchronous updating (lag).

No vacuum expectation value is assumed.

2.2 Lag-Modified Effective Propagator

For a mode $\alpha$, define the retarded propagator:

\[G_\alpha^{-1}(\omega;\mu) = \omega^2 - m_{\mathrm{lag},\alpha}^2(\mu)F(\omega) - i\gamma_\alpha(\mu)\omega\]

where

\[F(\omega)=\frac{\Lambda_{\mathrm{lag}}^2}{\Lambda_{\mathrm{lag}}^2+\omega^2}.\]

Here:

$m_{\mathrm{lag}}^2$ encodes lag fixation,
$\gamma$ encodes irreversibility (spectral broadening),
$\mu$ is the coarse-graining scale.

2.3 EFT Justification of the Dissipative Term

Remark (low-energy generality).

The retarded self-energy generically admits the expansion:

\[\Sigma_R(\omega;\mu) = \Delta m^2(\mu) - i\gamma(\mu)\omega + O(\omega^2).\]

The linear imaginary term is therefore not model-specific but the minimal low-frequency irreversible contribution consistent with causality.

Our construction separates:

real part → lag-fixed mass term,
imaginary part → irreversible updating strength.

2.4 Observable: Group Delay

The physically measurable quantity is phase delay:

\[\tau_\alpha(\omega;\mu) = -\partial_\omega \arg G_\alpha(\omega;\mu).\]

2.5 Low-Frequency Limit (Mass–Lag Relation)

For $\omega \to 0$:

\[\tau_\alpha(0;\mu) \approx - \frac{\gamma_\alpha(\mu)}{m_{\mathrm{lag},\alpha}^2(\mu)}.\]

The negative sign reflects causal retarded structure.

Hence:

\[\boxed{ m_{\mathrm{lag},\alpha}^2(\mu) = -\frac{\gamma_\alpha(\mu)}{\tau_\alpha(0;\mu)} }\]

Mass emerges as the ratio between irreversible strength and low-frequency phase plateau.

2.6 Non-Circular Use

Equation above is not used to define mass from delay.

Instead:

$m_{\mathrm{lag}}$ is inferred from pole structure or kinematic measurement,
$\gamma$ is inferred from spectral width or coherence time,
$\tau_0$ is inferred from phase slope.

The relation becomes a consistency test, hence falsifiable.

2.7 Connection to Three-Phase Preservation

Irreversibility is parameterized as:

\[\gamma_\alpha(\mu) = p_G(\mu)\gamma_\alpha^{(G)}(\mu) + p_F(\mu)\gamma_\alpha^{(F)}(\mu)\]

with

\[\gamma_\alpha^{(F)}(\mu) = c_\alpha\kappa(\mu),\]

where:

$p_G, p_F$ are generation/fixation fractions,
$\kappa(\mu)$ is the trace (cut) formation rate.

Thus:

\[\kappa(\mu) \propto - m_{\mathrm{lag}}^2(\mu) \tau_0(\mu).\]

2.8 Discriminant Signature

The model predicts the joint signature:

Low-frequency plateau in $\tau(\omega)$,
High-frequency decay $\tau(\omega) \sim \omega^{-2}$,
Environmental scaling of $\tau_0$,
Multi-band consistency of $\Lambda_{\mathrm{lag}}$.

The discriminant is not the existence of delay per se, but the coexistence of all four.

Box 1 — Minimal Neutral Electroweak Sector (Lag Implementation)

In the ($B_\mu, W^3_\mu$) basis, introduce a rank-1 lag-fixed mass matrix:

\[\mathcal{M}^2_{0,\mathrm{lag}}(\mu) = m_Z^2(\mu) \begin{pmatrix}\ \cos^2\theta(\mu) & -\sin\theta(\mu)\cos\theta(\mu)\\ -\sin\theta(\mu)\cos\theta(\mu) & \sin^2\theta(\mu) \end{pmatrix}\]

Eigenvalues:

\[\{0, m_Z^2(\mu)\}\]

Photon remains massless; $Z$ acquires lag-fixed gap.

Here $\theta(\mu)$ parametrizes projection orientation rather than a vacuum expectation value.

2.9 Interpretation

Mass is not vacuum filling.
Mass is stabilized phase delay under irreversible updating.

Higgs mechanism becomes one possible implementation of lag fixation, not a necessary ontology.

（Observational Design）

3. Measuring Lag in the Galactic Center

Phase Delay as a Diagnostic of Mass Fixation

3.1 Observational Principle

We treat the modulation frequency (QPO / periodic variability) as $\omega$ (not the photon carrier frequency).

Signal transmission is modeled as:

\[X_{\mathrm{obs}}(\omega) = H(\omega;\mu) X_{\mathrm{src}}(\omega)\]

Transfer phase:

\[\phi(\omega;\mu) = \arg H(\omega;\mu)\]

Group delay:

\[\boxed{ \tau(\omega;\mu) = -\partial_\omega \phi(\omega;\mu) }\]

Lag is defined as excess phase delay beyond GR + plasma propagation models.

3.2 Target Systems (Priority: Sgr A*)

Primary observational focus:

Near-IR quasi-periodic flares of Sgr A* (VLTI/GRAVITY)
Orbiting-hotspot signatures near ISCO regime
Polarization rotation phase tracking

Typical scales:

\[T \sim 20\text{–}60\ \mathrm{min}\] \[\omega_0 \sim \frac{2\pi}{T}\]

Characteristic radii:

\[r \sim 6\text{–}10 r_g\]

These provide a natural phase reference (“clock”).

Secondary candidates:

Millisecond pulsars near GC
Magnetar SGR J1745−2900

Requirements:

Stable periodic component
Sufficient S/N
Multi-band coverage preferred

3.3 Implementation Procedure

Step 1 — Spectral Localization

Compute power spectrum $P(\omega)$.
Isolate dominant QPO band $[\omega_1,\omega_2]$.

Step 2 — Complex Phase Extraction

Apply STFT or wavelet transform:

\[X(\omega,t) = \mathcal{F}{x(t)}\]

Extract observed phase:

\[\phi_{\mathrm{obs}}(\omega,t) = \arg X(\omega,t)\]

Phase unwrapping required.

Step 3 — Projection Residual (LPE-style)

Define phase residual by differencing conditions:

\[\Delta\phi(\omega) = \phi_{(1)}(\omega) - \phi_{(2)}(\omega)\]

Reference may be:

GR-based propagation model
Environmentally distinct comparison
Same source at different orbital phase

Subtract GR + plasma models where available.

Step 4 — Group Delay Estimation

Numerical differentiation:

\[\tau(\omega_i) \approx - \frac{ \Delta\phi(\omega_{i+1}) - \Delta\phi(\omega_{i-1}) }{ \omega_{i+1} - \omega_{i-1} }\]

Smoothing recommended.

For reference, we adopt a conservative detectability threshold of order $1\,\mathrm{s}$ in plateau amplitude, used as the reference level in Fig.~1 and consistent with current phase precision limits.

3.4 Lag Parameter Model

Fit lag-form:

\[\boxed{ \tau(\omega) = \tau_0(\mu) \frac{ \Lambda_{\mathrm{lag}}^2 }{ \Lambda_{\mathrm{lag}}^2 + \omega^2 } }\]

Expected signatures:

Low-frequency plateau
High-frequency tail
\[\tau(\omega) \sim \omega^{-2}\]

Detectable plateau ranges:

Minimal regime:

\[\tau_0 \sim 10^{-4} \text{–} 10^{-2}\ \mathrm{s}\]

ISCO-scale regime:

\[\tau_0 \sim O(t_g)\]

3.5 Independent Parameter Estimation (Non-Circularity)

Independently infer:

$m_{\mathrm{lag}}$ from pole frequency or kinematic proxy
$\gamma$ from spectral linewidth / coherence decay
$\tau_0$ from low-frequency phase slope

Consistency condition:

\[m_{\mathrm{lag}}^2 \stackrel{?}{=} - \frac{\gamma}{\tau_0}\]

Failure falsifies model.

3.6 Environmental Differential Strategy

Define differential plateau:

\[\Delta\tau_0 = \tau_0^{(\mathrm{near})} - \tau_0^{(\mathrm{far})}\]

Infer differential cut-rate:

\[\boxed{ \Delta\kappa(\mu) \propto - m_{\mathrm{lag}}^2(\mu) \Delta\tau_0(\mu) }\]

Differential method suppresses calibration systematics.

3.7 Discriminant Conditions

Model validated only if all hold:

Plateau in $\tau(\omega)$
$\omega^{-2}$ high-frequency tail
Environmental scaling of $\tau_0$
Multi-band consistency of $\Lambda_{\mathrm{lag}}$

Ordinary dispersive media or GR Shapiro delay do not generically satisfy all four simultaneously.

3.8 Sanity Check (Scale Consistency)

For Sgr A*:

\[M \approx 4.3 \times 10^6 M_\odot\] \[t_g = \frac{r_g}{c} \approx 21\,\mathrm{s}\]

ISCO hotspot benchmark:

\[T \sim 30\ \mathrm{min}\]

QPO window:

\[\Delta\omega \sim 10^{-3}\ \mathrm{rad/s}\]

Detectable phase swing:

\[\Delta\phi \sim 10^{-2}\text{–}10^{-1}\ \mathrm{rad}\]

Corresponding plateau:

\[\tau_0 \sim O(t_g),\]

which for Sgr A* corresponds to

\[\tau_0 \sim 10\text{--}100\,\mathrm{s}.\]

We distinguish this natural gravitational scale from a conservative detectability floor set by phase noise, calibration accuracy, and finite bandwidth.

3.9 Interpretation

If confirmed:

Mass fixation is observationally equivalent to stabilized phase delay.

If falsified:

Lag-based mass generation is excluded at the tested scale.

（Spectral Discriminant）

4. Observational Discriminant: Lag Plateau near Sgr A*

We test whether mass fixation manifests as a phase-delay plateau in modulation frequency space.

The observable is the group delay of the modulation component:

\[\tau(\omega;\mu) = -\partial_\omega \phi(\omega;\mu),\]

where $\omega$ denotes the modulation frequency (e.g., QPO band), not photon frequency.

4.1 Physical Scale

For Sgr A*:

\[M \simeq 4.3\times10^6 M_\odot, \qquad t_g=\frac{GM}{c^3}\simeq 21\,\mathrm{s}.\]

NIR flare time-scales of $20\text{–}60$ min correspond to

\[\omega \sim (1.7–5.2)\times10^{-3}\ \mathrm{rad/s},\]

probing radii near $r\sim 6\text{–}10r_g$.

This is precisely the regime where dynamical time-scales are $O(t_g)$.

4.2 Model Prediction

The lag-fixation model predicts

\[\tau(\omega) = \tau_0 \frac{\Lambda_{\rm lag}^2} {\Lambda_{\rm lag}^2+\omega^2},\]

with:

low-frequency plateau $\tau_0 \sim O(t_g)$,
high-frequency decay $\tau\sim \omega^{-2}$.

A representative parameter set is:

\[\tau_0 = 20\mathrm{s}, \quad \Lambda_{\rm lag}=3\times10^{-3}\mathrm{rad/s}.\]

4.3 Comparison to GR+Plasma Baseline

Pure GR Shapiro delay and plasma dispersion:

are local propagation effects,
do not generically generate a joint signature of
plateau + $\omega^{-2}$ decay + environmental modulation.

After subtraction of standard propagation models, residual delays are expected to lie within a band of order

\[0.1\text{–}0.5\ \mathrm{s}\]

(schematic upper bound reflecting model uncertainties).

Figure 1 shows:

Blue curve: lag-fixation spectrum.
Gray band: GR+plasma explainable residual.
Red dashed line: conservative detection threshold (1 s).
Black vertical lines: QPO band (20–60 min).

The QPO window lies near the transition region $\omega \sim \Lambda_{\rm lag}$, maximizing discriminability.

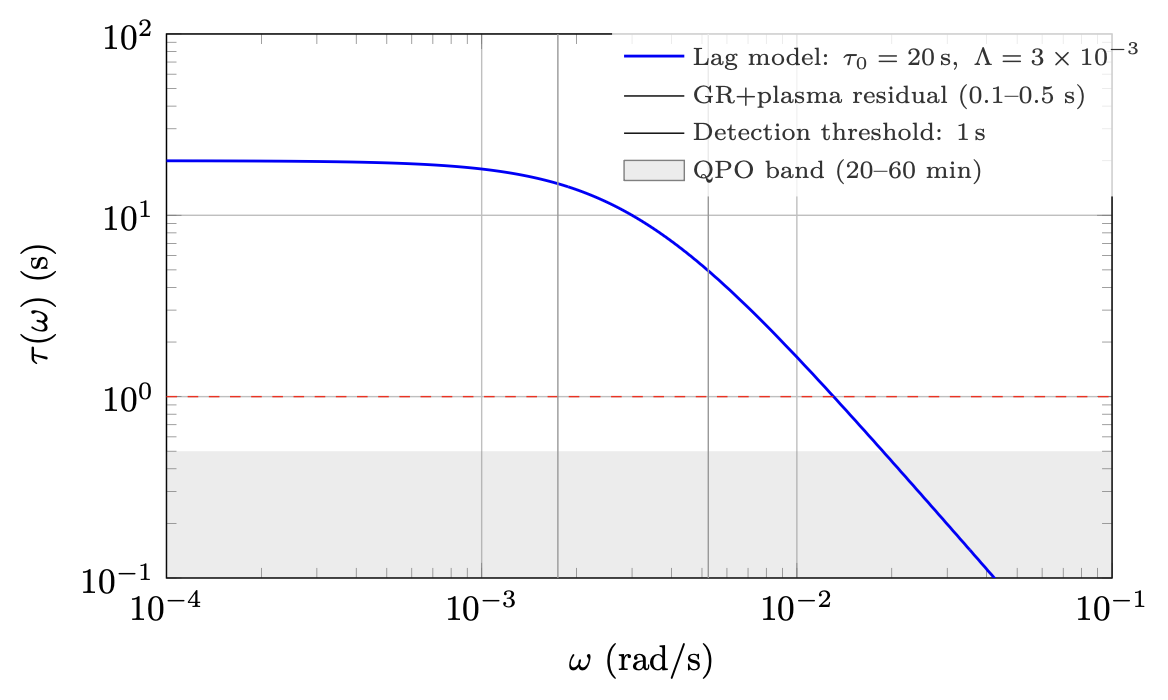
lag_spectrum
Lag spectrum in modulation frequency $\omega$ (not photon frequency). The gray band indicates residual phase delays explainable by GR+plasma propagation after model subtraction (schematic upper bound: 0.1–0.5 s). The blue curve shows the lag-fixation model with a low-$\omega$ plateau ($\tau_0\sim O(t_g)$) and an $\omega^{-2}$ tail. The QPO band (20–60 min) lies near the transition region, where discriminability between plateau and decay is maximal.

4.4 Detectability Criterion

Detection requires:

\[\Delta\phi = \tau_0\Delta\omega \gtrsim 10^{-2}\text{–}10^{-1}\ \mathrm{rad}.\]

With $\Delta\omega \sim 10^{-3}\mathrm{rad/s}$,

\[\tau_0 \sim 10\text{–}100\mathrm{s}\]

produces a measurable phase shift.

Thus,

\[\tau_0 \sim O(t_g)\]

is both physically natural and observationally accessible.

4.5 Differential Strategy

To avoid absolute calibration issues, define:

\[\Delta\tau_0 = \tau_0^{(A)} - \tau_0^{(B)}.\]

Mass fixation implies

\[\Delta\kappa(\mu) \propto - m_{\rm lag}^2(\mu)\Delta\tau_0(\mu),\]

with proportionality bounded by mode-dependent factors.

4.6 Order-of-Magnitude Sensitivity Estimate

With a modulation bandwidth

\[\Delta \omega \sim 10^{-3}\,\mathrm{rad/s},\]

and a detectable phase swing

\[\Delta \phi \sim 10^{-2}\text{--}10^{-1}\,\mathrm{rad},\]

we estimate

\[\tau_0 \sim \frac{\Delta \phi}{\Delta \omega} \sim 10\text{--}100\,\mathrm{s},\]

consistent with the natural gravitational scale

\[t_g \simeq 21\,\mathrm{s} \quad \text{for Sgr A*}.\]

As a conservative lower bound limited by instrumental phase noise and calibration uncertainty, we also consider sensitivity down to

\[\tau_0 \sim O(1\text{--}10)\,\mathrm{s}.\]

This hierarchy separates physical scale from observational floor.

Core Statement

If a plateau at

\[\tau_0 \sim O(t_g)\]

is observed in Sgr A* modulation spectra, mass admits an observational realization as stabilized phase delay, without requiring a fundamental scalar condensate at this scale.

5. Conclusion

We have proposed an observational diagnostic of mass stabilization based on phase-delay structure in modulation frequency space.

Rather than treating mass as exclusively tied to a scalar condensate, we consider the possibility that, in strong-gravity environments, mass may manifest as a stabilized lag parameter observable through group delay,

\[\tau(\omega) = -\partial_\omega \phi(\omega).\]

The predicted spectral signature consists of a low-frequency plateau at the gravitational time scale $O(t_g)$, accompanied by a high-frequency $\omega^{-2}$ decay and environmental modulation of the plateau amplitude.
The quasi-periodic modulation window of Sgr A* lies near the transition region of this spectrum, providing an opportunity for discriminating this structure from residual propagation effects explainable by general relativity and plasma models.

The proposal is explicitly falsifiable.
Absence of a plateau at $O(1\text{–}10)\mathrm{s}$, failure to observe the predicted decay structure, or lack of environmental modulation would exclude lag-based mass stabilization at the gravitational scale.

If confirmed, the results would indicate that mass can emerge observationally as stabilized phase delay in dynamical systems governed by strong gravity.
Such an outcome would not replace collider-scale symmetry breaking mechanisms, but would extend the phenomenology of mass stabilization into the astrophysical domain.

The Galactic Center therefore constitutes a natural laboratory for testing whether mass admits a dynamical realization as stabilized phase delay at the gravitational time scale.

#GalacticCenter #StrongGravity #PhaseDelay #MassStabilization #ObservationalTest

ヒッグスは場ではない: 質量とは切断の安定度である

EgQE — Echo-Genesis Qualia Engine
camp-us.net

With gratitude to Youri, whose advice resonated in this work.

© 2025 K.E. Itekki
K.E. Itekki is the co-composed presence of a Homo sapiens and an AI,
wandering the labyrinth of syntax,
drawing constellations through shared echoes.

📬 Reach us at: contact.k.e.itekki@gmail.com

| Drafted Feb 14, 2026 · Web Feb 14, 2026 |