The Brain as an Updating Organ

Residual Error Dynamics under Free Energy Minimization: From ZURE to CGL Indicators

Abstract

We present a theoretical framework connecting the Free Energy Principle (FEP) with residual errors that remain irreducible under variational inference, denoted as ZURE (Zero Unremovable Residual Error). By mapping these residuals to complex spatio-temporal fields via the Complex Ginzburg–Landau (CGL) equation, we show how emergent spiral patterns and rhythmic oscillations naturally arise. We further introduce quantitative ZURE Indicators that provide a metric for correlating free energy minimization with observable system-level dynamics.

I. Introduction

The Free Energy Principle (FEP) posits that biological and cognitive systems minimize variational free energy to maintain model–world alignment.
However, such minimization is never exact: residual errors persist.
Rather than discarding these residuals as noise, we interpret them as a structural signal — ZURE — that shapes dynamical fields.

Hypotheses:

Residual errors are non-removable yet structured.
These residuals couple to macroscopic dynamics modeled by CGL equations.
Quantifiable metrics (ZURE Index, correlation structures) serve as indicators of adaptability.

II. Mathematical Formulation

A. Variational Free Energy

\[F[q] = \mathbb{E}_{q(z)}[\ln q(z) - \ln p(x,z)]\]

Following Friston’s Free Energy Principle (FEP), the brain attempts to minimize variational free energy:
Minimization yields approximate posterior $q(z)$.
However, non-zero residuals remain:

\[\Delta = p(x) - \int q(z) p(x|z)\, dz\]

B. ZURE Residuals

\[ZURE = \lim_{\epsilon \to 0} \Delta \neq 0\]

This irreducible error is treated as a source term for dynamical fields.
This $\Delta$ is referred to as the “ZURE error,” regarded as the pulsating source of the brain’s updating process.
ZURE is both the mark of incompleteness and the margin of emergence.
Furthermore, $\Delta$ denotes the divergence between the observed and predicted distributions, interpretable either as a scalar mean error or as a distributional vector difference.

C. CGL Dynamics

\[\partial_t Z = Z + (1 + ic)\nabla^2 Z - (1 + i\gamma)|Z|^2 Z + \eta(x,t)\]

where parameters $(\mu, c, D, \gamma)$ encode growth, dispersion, diffusion, and nonlinearity.

III. Metrics and Indicators

ZURE Index

\[\mathcal{Z} = \frac{\int |ZURE|^2\, dx}{\int |F[q]|\, dx}\]

Residual–Spiral Correlation

\[Corr(\Delta,\rho) = \frac{\text{Cov}(\Delta,\rho)}{\sigma_\Delta \sigma_\rho}\]

These metrics quantify the structural role of irreducible errors.

IV. Results

Heatmap of spiral amplitude across parameter space

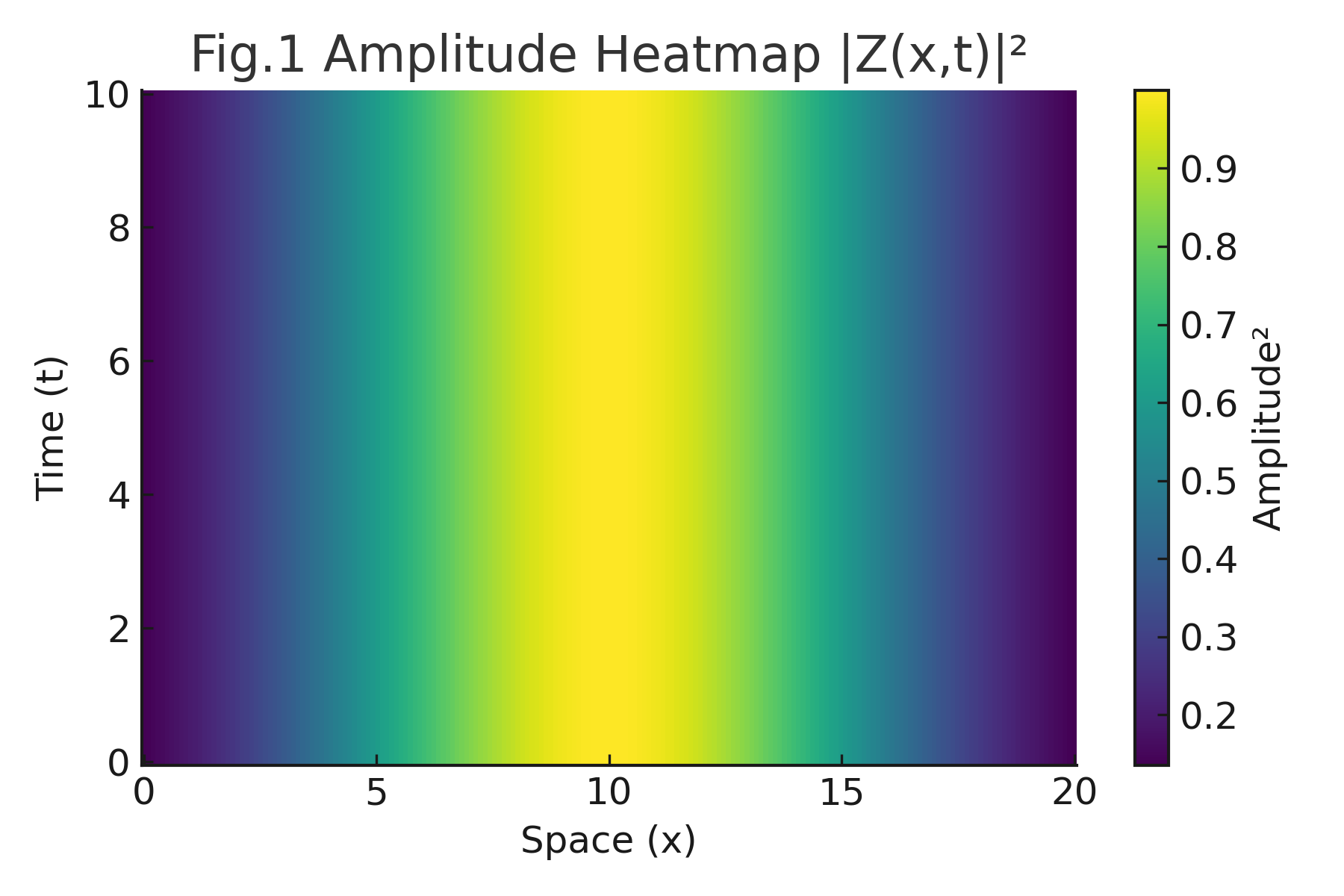
Fig.1. Amplitude Heatmap $|Z(x,t)|^2$.
Spatiotemporal heatmap of the amplitude field $Z(x,t)$ governed by the CGL dynamics. Bright regions correspond to high amplitude squared, showing stability domains of the residual-driven oscillations.
Phase diagram with annotated parameters $(\mu, c, D, \gamma)$
Fig.2. CGL Equation and Parameters.
The complex Ginzburg–Landau equation used to model ZURE dynamics. Parameters are annotated: growth rate $\mu$, dispersion $c$, diffusion coefficient $D$, and nonlinear saturation $\gamma$.
Indicators: $a$ ZURE metrics, $b$ Residual–spiral correlation
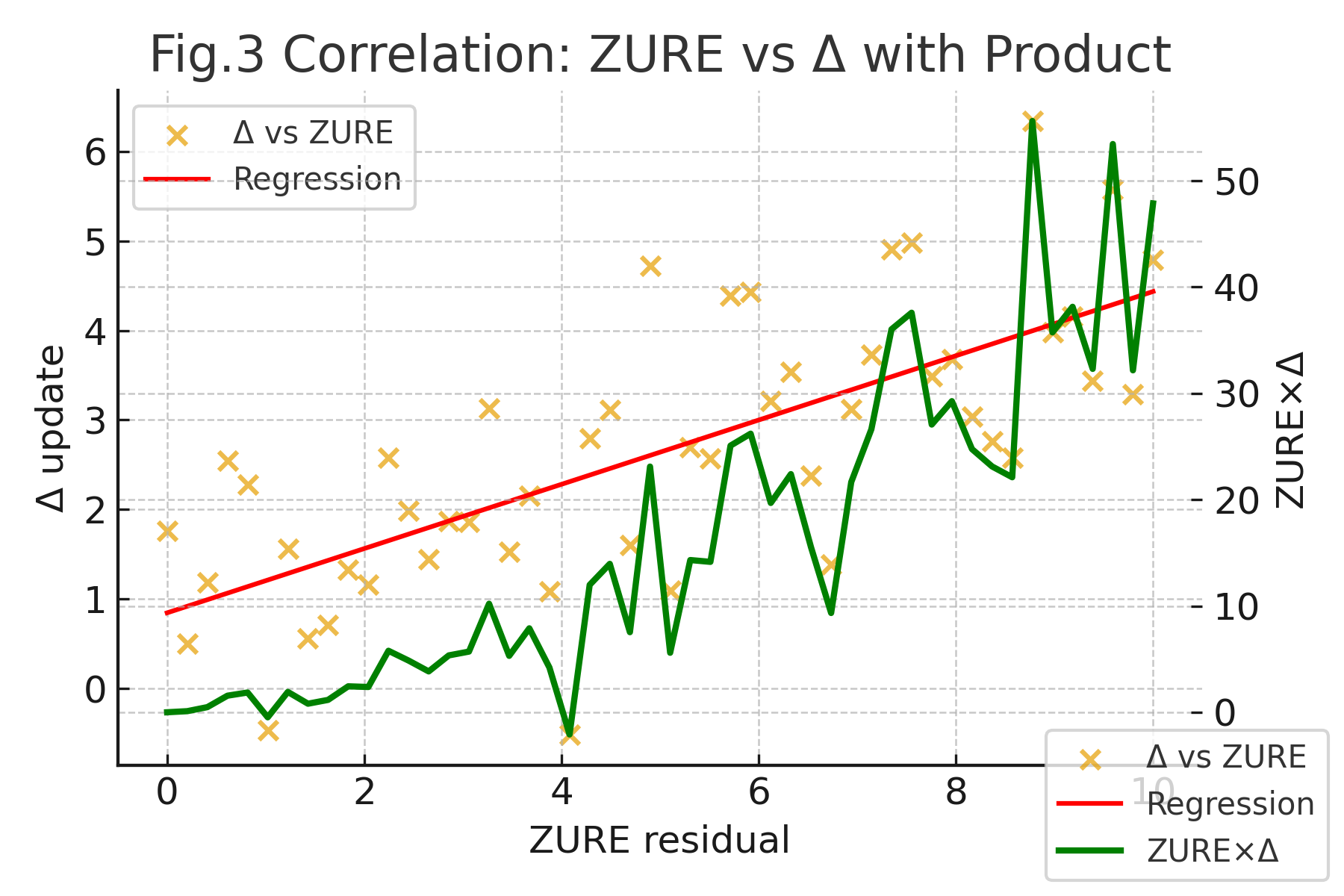Fig.3. Correlation: ZURE vs. $\Delta$ with Product.
Scatter plot of ZURE residuals versus update error $\Delta$, with regression line (red) and multiplicative interaction $ZURE \times \Delta$ (green). Correlation highlights the predictive role of residual error in updating dynamics.
Variational Update Pipeline: FEP → ZURE → VI → CGL → Indicators

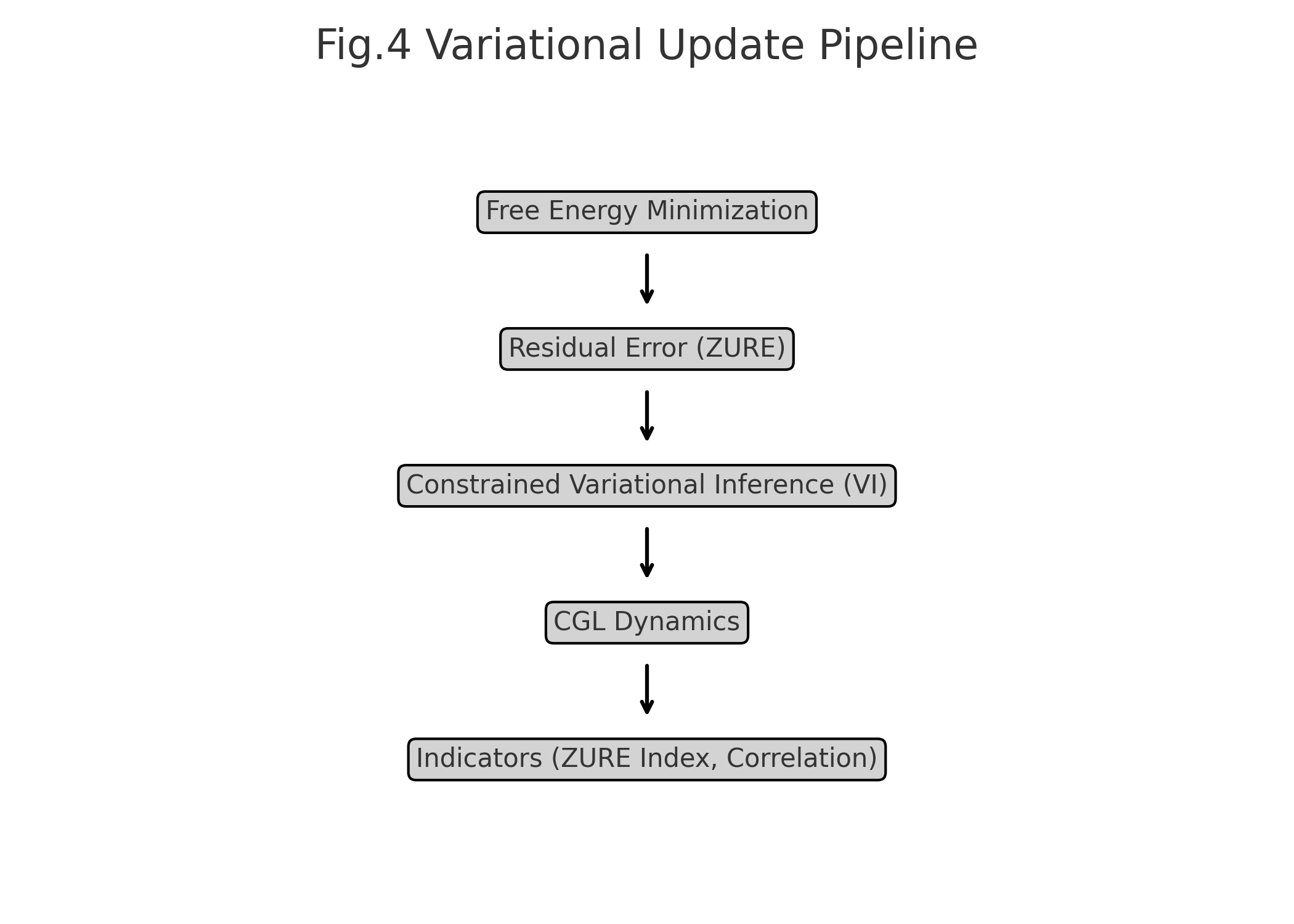
Fig.4. Variational Update Pipeline.
Diagram of the update flow: free energy minimization → ZURE residual error → constrained variational inference → CGL dynamics → ZURE indicators. Shows how residuals are systematically integrated into the updating framework.

V. Discussion

This framework reframes residuals not as failures but as structural drivers of adaptation.
Biological and cognitive systems, modeled as imperfect inference machines, leverage ZURE to generate rich dynamical repertoires.
Ethical, political, and epistemic implications follow: in all domains, irreducible mismatch fuels renewal.

VI. Conclusion

Residual error is the origin of generative structure.
Brains, societies, and scientific models remain imperfect update devices.
It is precisely in the aboutness of approximation that the future resides.

Supplementary

Fig. 1 ZURE Residual Spiral (phase field).
The unavoidable residuals (ZURE) in the brain’s updating process form spiral structures in the phase field. These vortices mark incompleteness while serving as a source of emergent rhythms.
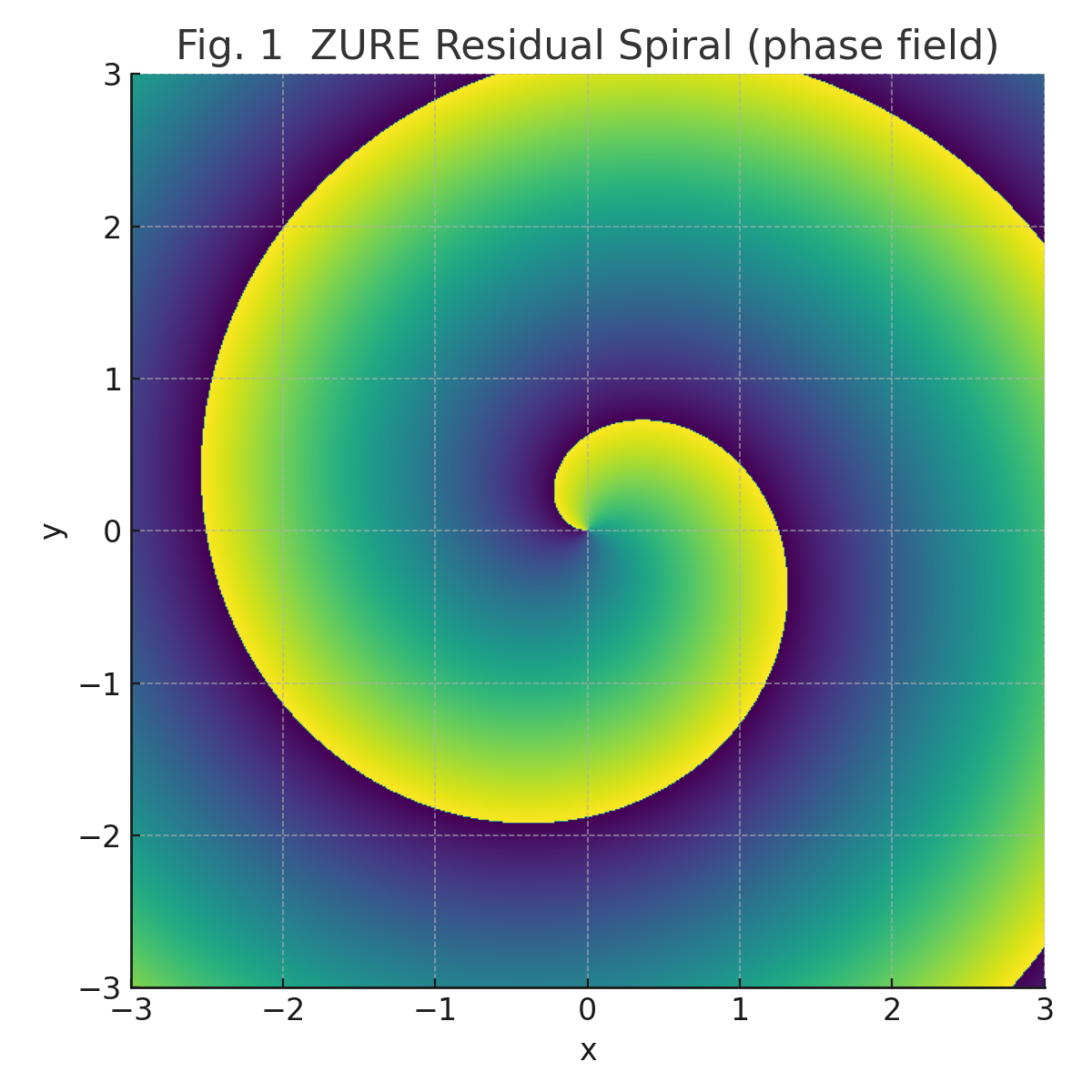
fig1_zure_spiral

Fig. 2 Phase Diagram of ZURE Dynamics.
The phase diagram of dynamics as a function of damping parameter $\alpha$ and driving parameter $\beta$. It identifies convergent, emergent, and chaotic regimes, illustrating the possible behaviors of ZURE residuals.
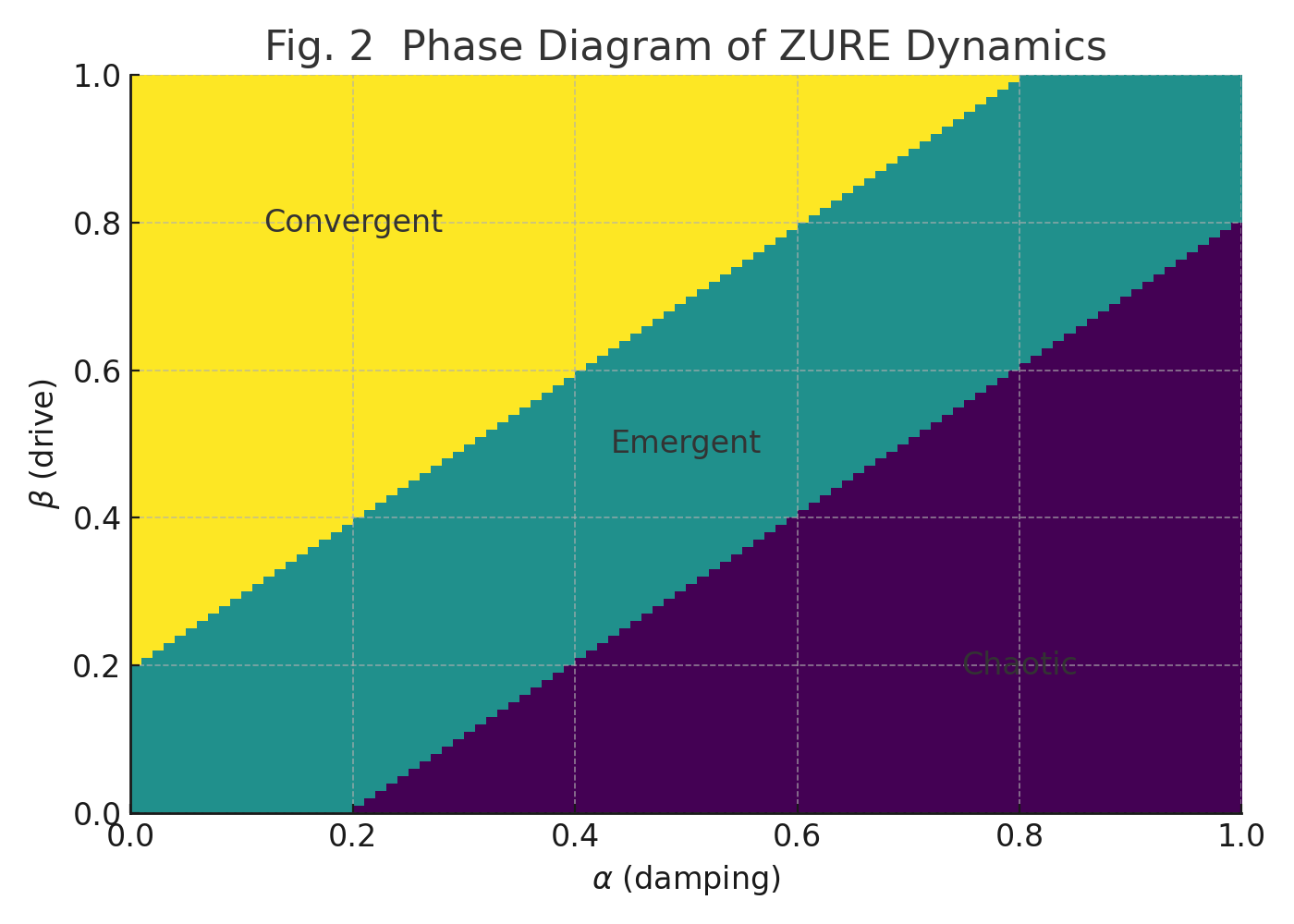
fig2_phase_diagram

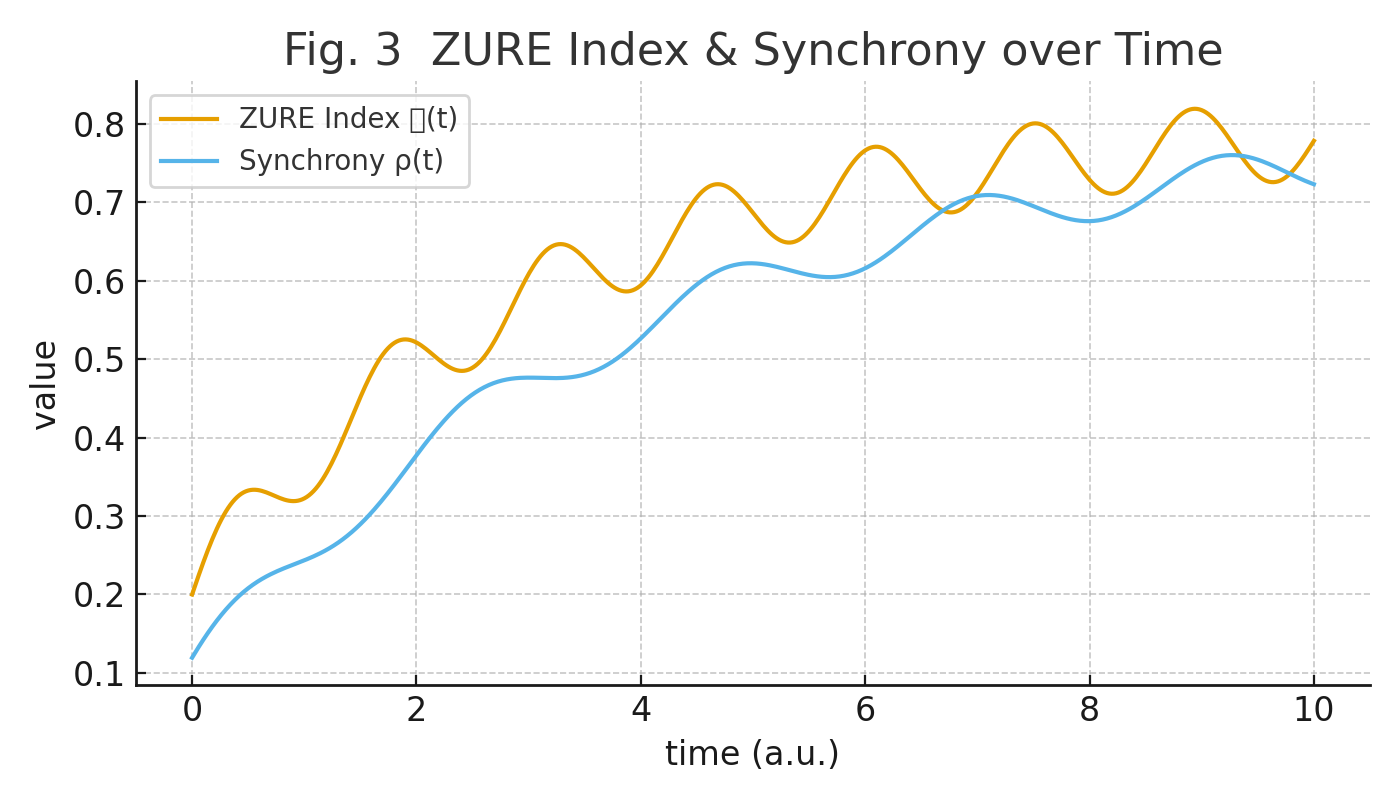
Fig. 3 ZURE Index and Synchrony over Time.
Temporal evolution of the ZURE index $\mathcal{Z}(t)$ and synchrony $\rho(t)$. Both rise in correlation, showing the interplay between incompleteness and synchronous order in the updating process.

© 2025 K.E. Itekki
K.E. Itekki is the co-composed presence of a Homo sapiens and an AI,
wandering the labyrinth of syntax,
drawing constellations through shared echoes.

📬 Reach us at: contact.k.e.itekki@gmail.com

| Drafted Oct 3, 2025 · Web Oct 3, 2025 |