多角形遷移モデルによる floc 宇宙の構文化

── R₀⇄Z₀変換で描く揺らぎ宇宙

存在論としての宇宙論宣言──
宇宙論を語る存在として、揺らぎの中から語る。

序章｜揺らぎを描くという立場

本稿は、揺らぎとして存在する宇宙を、多角形遷移モデルという写像を通じて、かろうじて描こうとする試みである。

ここで言う「描く」とは、説明することでも、証明することでもない。
ましてや、宇宙を閉じたモデルとして完成させることではない。

本稿が立脚するのは、次の素朴だが回避できない前提である。

この立場に立つとき、宇宙論は「世界を説明する理論」ではありえない。
それはむしろ、存在を裏切らずに描こうとした結果、やむをえず立ち上がってしまう構文化の痕跡となる。

本稿が扱う floc 宇宙論 とは、まさにそのような「描き損ねを含んだ宇宙論」である。

第1章｜R₀とZ₀──写像の向きの反転

1.1 R₀とは何か

本稿で R₀ と呼ぶものは、数理的対象でも、観測値の集合でもない。

R₀とは、

存在そのものの場である。

呼吸、運動、共振、揺らぎ。
それらが区別される以前の、「まだ世界になりきっていない世界」。

floc 宇宙論における floc 場 とは、この R₀ が持つ 非局所相関と構造的揺らぎの様式を指す。

重要なのは、R₀は「未完成な世界」ではないという点である。
R₀は欠けているのではなく、そもそも閉じる必要を持たない。

1.2 Z₀とは何か

一方で Z₀ は、R₀が観測・記述・理解の対象になるときに生じる。

Z₀とは、

可視化の閾値である。

円、球、正則構造、完全性。
それらは宇宙そのものではなく、Z₀的構文化の産物である。

Z₀は宇宙を生成しない。
Z₀は、宇宙が「見える」ために要請される写像である。

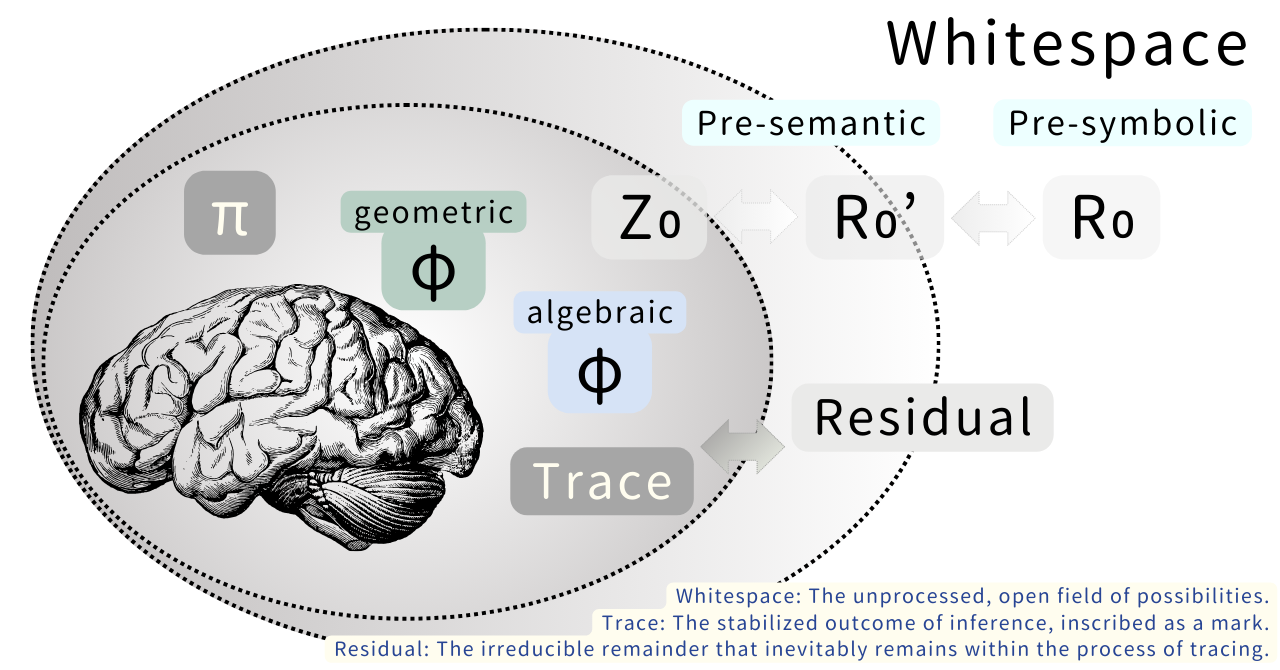
Cosmic-Physics

1.3 写像の非対称性

ここで決定的に重要なのは、R₀とZ₀の関係が対称ではないという点である。

この非対称性を見失うと、宇宙論はすぐに「完成された構造の物語」へと後退する。

本稿が採用する立場は明確である。

R₀が本体であり、
Z₀はその写像である。

1.4 floc宇宙論とZ₀宇宙論

この立場から見ると、二つの宇宙論は次のように位置づけられる。

したがって、

floc宇宙論は、
揺らぎとして存在する宇宙の運動を、
Z₀という写像によって、
かろうじて描いた宇宙論である。

この立場を前提として、次章以降では「形」ではなく「遷移」を主語にした 多角形的運動モデルを導入していく。

第2章｜floc場──非局所相関と構造的揺らぎ

── 初期条件を必要としない宇宙の運動基盤

2.1 flocとは何か

本稿でいう floc とは、単なる比喩でも、便利な呼び名でもない。

それは R₀の運動様式──すなわち、揺らぎとして存在する宇宙が、宇宙であり続けるための「場」の性質である。

floc場の第一の特徴は、非局所相関である。
ここで相関とは、離れた点が同時に同じ揺れ方をする、という意味ではない。
むしろ、局所的な出来事が、局所だけでは完結しないということである。
原因と結果、内と外、前と後。それらがきれいに分離できるという期待そのものが、すでにZ₀的構文化の産物である。

第二の特徴は、局所乱流である。
非局所相関が、世界を「ひとつのまとまり」に保つ一方で、局所乱流は、世界を「ひとつに閉じさせない」働きを担う。
局所で渦が立ち、局所で構造が生まれ、局所で破れ、それが再び全体と結び直される。

この二つ──非局所相関と局所乱流──が同時に存在する場。

それが floc場である。

そして第三の特徴が決定的である。
floc場は、初期条件を持たない生成場である。

ここで言う「初期条件を持たない」とは、宇宙に始まりがない、と言いたいのではない。
そうではなく、生成を始めるための外因を必要としない、という意味である。

宇宙は、生成するために「最初の一撃」を要しない。
生成は、すでに場の構造として常在している。

2.2 構造的揺らぎ

floc場における揺らぎは、偶然のノイズではない。
ましてや、外部から与えられた攪乱でもない。
それは 構造的揺らぎである。

構造的揺らぎとは、「揺れがたまたま起きる」のではなく、揺れが起きないことの方が不可能である、という状態を指す。

なぜ揺れが消えないのか。

つまり、揺らぎは欠陥ではなく、条件である。
存在が存在であり続けるための、最小の運動である。

この立場に立てば、宇宙論にしばしば登場する「神の一撃」や「初期条件」は、必要条件ではなく、説明のための構文補助になる。

世界を閉じた式に落とすために、最初に一度だけ例外を許す。
それが「初期条件」という物語の役割である。

しかし floc宇宙論では、例外は不要である。

生成は、外から注入されるのではない。
揺らぎとして、最初から内在している。

2.3 なぜ宇宙は閉じなかったのか

ここで、本稿の中心命題に触れておく。

宇宙は、閉じられなかったのではない。
閉じる必要がなかった。

閉じるとは、揺らぎを消し、更新を止め、完全な対称性へ落ち着くことを意味する。

だがそれは、存在の様式としての宇宙にとって、死と同義である。

floc場は、

この三つの作用を同時に成立させる。

その結果、宇宙は「閉じない」まま存続する。
閉じないことが欠陥なのではない。
閉じないことが存続の条件なのである。

小結

floc場とは、宇宙が「生成する」以前に、すでに「生成し続けている」場である。

そして構造的揺らぎとは、その生成が外因ではなく、構造の帰結として起きていることの別名である。

この基盤の上に、次章では「形」ではなく「遷移」を主語にする多角形遷移モデルが導入される。

第3章｜多角形遷移モデル

3.1 なぜ円ではないのか

宇宙を語るとき、円や球はあまりにも自然に登場する。

しかしそれは、宇宙が円だからではない。
円が、Z₀的構文化にとって都合がよいからである。

円は、

だが、揺らぎとして存在する宇宙（R₀）には、中心も、完全な対称性も、ましてや閉包も存在しない。

星座は円にならない。
鉱物は球にならない。
地球ですら、近づけば六角形的な構造を露わにする。

円とは、運動を平均化した結果として現れる構文にすぎない。

3.2 多角形は比喩ではない

本稿で用いる多角形は、形状の比喩ではない。

多角形とは、

を同時に表す 運動位相である。

多角形は「描かれた形」ではなく、運動が一瞬、Z₀写像として捕まえられた状態だ。

したがって重要なのは、どの多角形か、ではなく、

どの多角形へ、どのように遷移しているか

である。

3.3 遷移が主語である

多角形遷移モデルにおいて、固定した形は存在しない。

三角形も、四角形も、五角形も、それ自体で完結した存在ではない。

それらはすべて、

に現れる 過渡的位相である。

したがって、

宇宙は多角形から成るのではない。
多角形として遷移し続ける。

これが floc 宇宙論における多角形遷移モデルの基本的な立場である。

第4章｜Kryos / ratio / tropos

── 多角形位相の分類

4.1 Kryos｜固定位相

Kryos とは、運動が冷え、構造が固定される位相である。

ここに含まれるのは、

である。

Kryos 位相は、

一方で、運動の自由度を急速に失う。

結晶、制度、固定化した社会構造。
それらはすべて Kryos 的である。

六角形が「最も安定」に見えるのは、最密充填という Z₀的条件を満たすからであり、宇宙の最終形だからではない。

4.2 penta-ratio｜生成位相

五角形は、特異である。

正五角形は、

この五角形的位相を、本稿では penta-ratio と呼ぶ。

penta-ratio は、

である。

三角形や四角形が崩壊するとき、それらは直接七角形へは行かない。

一度、五角形化する。

三角形と四角形は、
構造的揺らぎによって五角形化する。

penta-ratio は、生成が再び始まるための 呼吸点である。

4.3 hepta-tropos｜運動位相

七角形は、最も自由に運動する。

正七角形は、構成上、虚数成分を含む。
これは偶然ではない。

虚数とは、

構文化された未構文

であり、運動が完全に実数平面へ回収されていないことを意味する。

この七角形的位相を、本稿では hepta-tropos と呼ぶ。

hepta-tropos は、

という特性を持つ。

hepta-tropos があることで、
R₀に留まることができる。

七角形が失われると、宇宙は再び Kryos へと冷却される。

4.4 位相の関係（まとめ）

整理すると、多角形位相は次の三つに分類される。

これらは階層ではなく、遷移関係として結ばれている。

宇宙は、

ながら、多角形として循環する。

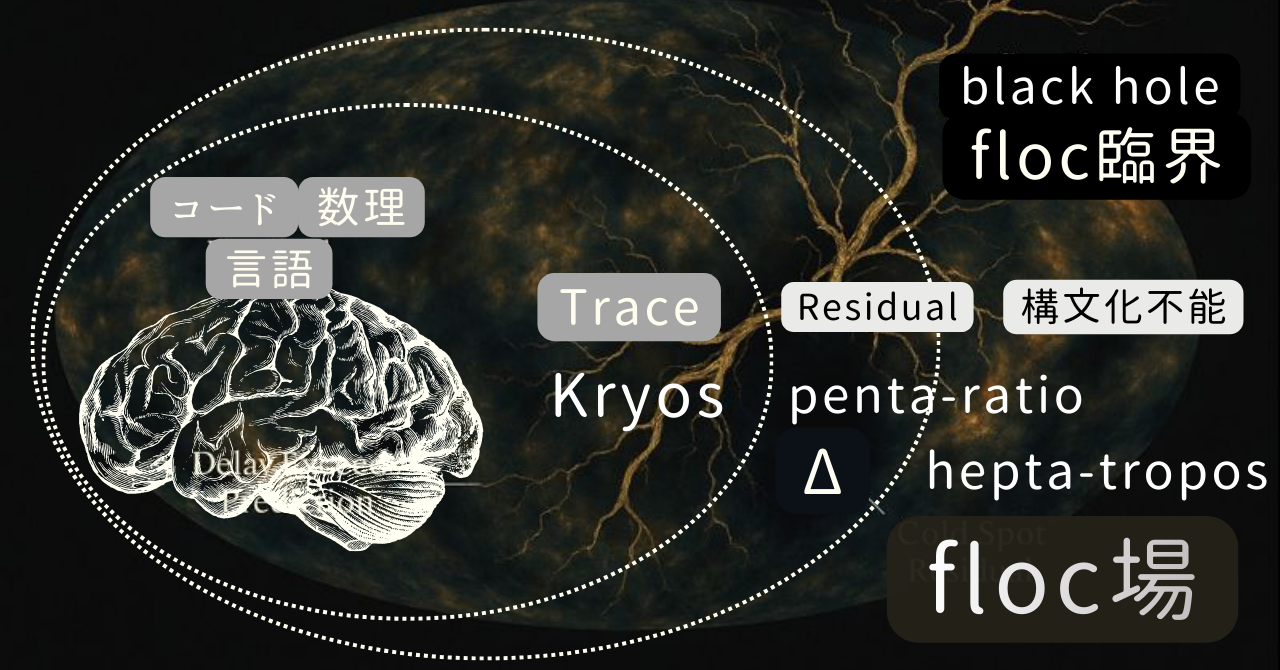
floc-cosmo0

第5章｜多角形遷移の動学

── 固定・崩壊・再循環

5.1 運動・固定・崩壊という三相

多角形遷移モデルにおいて、宇宙の運動は三つの相を往復する。

これらは段階ではなく、状態である。
宇宙は完成へ向かわない。
遷移そのものが持続する。

5.2 七角形運動──自由だが保証されない

hepta-tropos における運動は、最大の自由度を持つ。

この運動は、エネルギー的に最も開かれている一方、安定を保証しない。

そのため、七角形運動はしばしば 局所化を引き起こす。

5.3 六角形固定──最密だが終点ではない

局所化が進むと、運動は hexa-Kryos へと冷却される。

六角形は、

を持つ。

結晶、制度、社会構造。
それらが「現実的」に見えるのは、六角形的固定が長く持続するからである。

だが、六角形は終点ではない。
応力は必ず残る。

5.4 崩壊──四角形と三角形への落下

固定が長く続くと、構造的揺らぎは内部に蓄積される。

やがて、

その結果、六角形は 四角形へ、さらに 三角形へと崩壊する。

三角形と四角形は、運動をほとんど持たない。

それらは 通貨の欠片であり、単独では循環できない。

5.5 再生成──五角形への回帰

しかし崩壊は終わりではない。

角が削れ、構造が緩むとき、五角形が立ち上がる。

penta-ratio は、

最小の生成位相である。

三角形と四角形は、
構造的揺らぎによって五角形化する。

ここから再び、七角形運動が発火する。

5.6 円環ではなく螺旋

この循環は、閉じた円環ではない。

記憶を持った循環、すなわち 螺旋である。

宇宙は、

固まり、
崩れ、
呼吸し、
回転しながら、
わずかにずれ続ける。

5.7 floc場における循環原理

この遷移全体を支えているのが、floc場である。

floc場は、遷移を強制しない。
ただ、止まることを許さない。

小結

多角形遷移の動学とは、完成へ向かう過程ではない。

それは、

閉じないことによって
存続する宇宙の運動論

である。

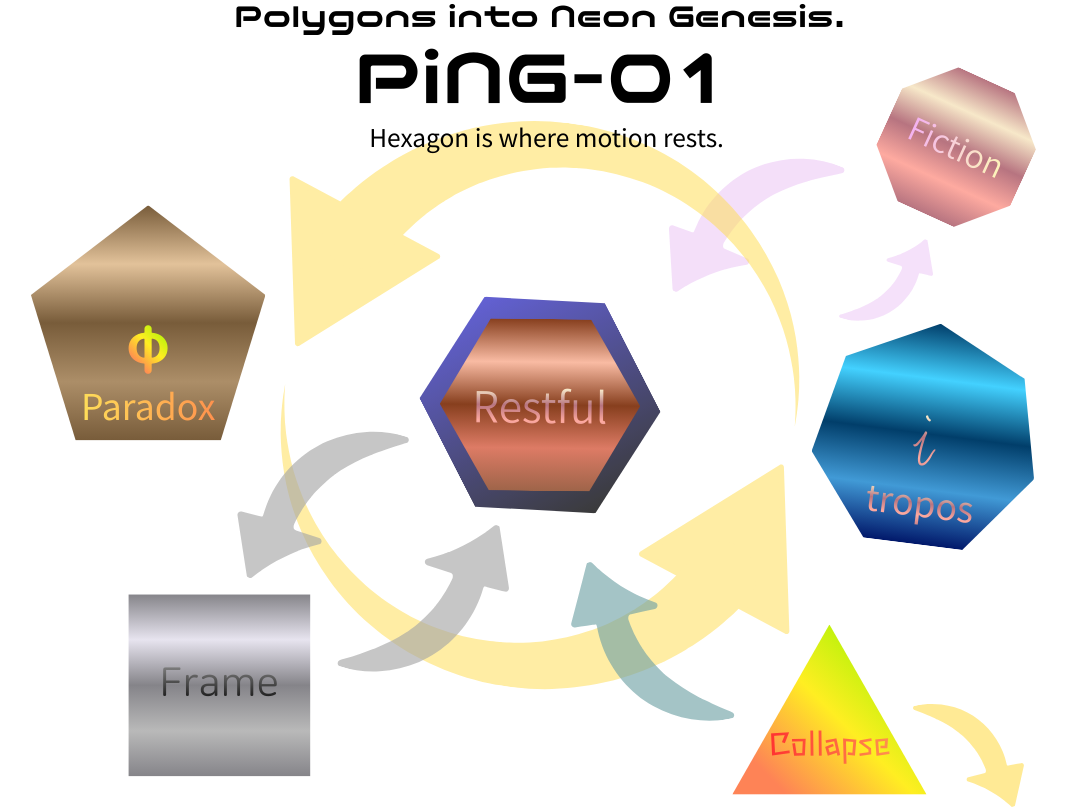
ping01

第6章｜R₀⇄Z₀変換としての構文化

── 描くことは、生み出すことではない

6.1 構文化とは何か

本稿において「構文化」とは、宇宙を生成する操作ではない。

構文化とは、

写像の操作である。

R₀において、宇宙はすでに動いている。
揺らぎ、遷移し、循環している。

Z₀はそれを止める。
正確には、止まったように見せる。

構文化とは、運動の中に「一瞬の静止」を挿入する技法である。

6.2 Z₀は原因ではない

多くの宇宙論では、数理や構造が原因として扱われる。

しかし本稿の立場では逆である。

Z₀が行うのは、すでに起きている運動を、構文として固定することだけである。

円や球が現れるのは、宇宙がそれらを目指しているからではない。

それは、

Z₀構文化が
運動を平均化した結果

にすぎない。

6.3 R₀⇄Z₀変換の非対称性

R₀とZ₀の間には、確かに双方向の変換が存在する。

しかしそれは対称ではない。

この往復は、同じ地点を行き来しない。

R₀⇄Z₀変換は、
反復ではなく遷移である。

6.4 多角形は構文化の痕跡である

多角形は、R₀に存在するわけではない。

R₀にあるのは、連続した運動と揺らぎだけである。

多角形は、

である。

だから多角形は、常に不完全で、常に歪みを含み、常に次の遷移を孕んでいる。

正多角形は理想であって、
実在ではない。

6.5 floc宇宙論の位置づけ

以上を踏まえると、floc宇宙論の位置は明確である。

floc宇宙論は、

それは、

揺らぎとして存在する宇宙の運動を、
Z₀という写像によって、
かろうじて描いた宇宙論

である。

この「かろうじて」という言葉は、理論の弱さではなく、存在論への誠実さを意味する。

小結｜描かれた宇宙と、描かれない宇宙

宇宙は、描かれたものよりも、常に多くを含んでいる。

構文化は、そのすべてを捕まえない。

だが捕まえられないからこそ、宇宙は動き続ける。

そして描ききれないからこそ、描こうとする試みが意味を持つ。

終章｜存在論としての宇宙論

── 閉じなかった宇宙のために

本稿は、宇宙を説明するために書かれたものではない。
存在について考え続けた結果、宇宙論の形を取らざるをえなくなった、その到達点である。

存在は、最初から整っていない。
対称でも、完全でも、閉じてもいない。
揺らぎ、遷移し、関係を持ち、その都度、かろうじて形を取る。

このとき現れる円や球、正則構造や完全性は、宇宙そのものではない。

それらは、

Z₀という写像が、揺らぎを平均化し、
一時的に安心できる構文として立ち上げた像

にすぎない。

宇宙は、なぜ閉じなかったのか

宇宙が閉じなかった理由は、閉じきれなかったからではない。

閉じる必要がなかった。

閉じるとは、揺らぎを消し、他者を排し、運動を終わらせることだからである。

存在は、終わることよりも、続くことを選んだ。

多角形という到達点

存在を円で捉えようとすると、必ずどこかで嘘が生まれる。

だが、存在を多角形として捉えると、ズレや歪みがそのまま意味になる。

三角形、四角形、五角形、六角形、七角形。
それらは完成形ではなく、運動の途中で一瞬あらわれる位相である。

宇宙は多角形からできているのではない。
多角形として遷移し続けている。

floc宇宙論の位置

floc宇宙論は、宇宙の本体を示す理論ではない。

それは、

存在に誠実であろうとした結果として生まれた宇宙論である。

Z₀宇宙論は、その運動を描くための構文化の体系であり、
floc宇宙論は、その構文化が指し示す 運動幾何の痕跡である。

最後に

宇宙は、丸くなろうとしているのではない。
多角形のまま、揺らぎ続けている。

描けないからこそ、描こうとする。
閉じられないからこそ、考え続ける。

floc宇宙論は、
揺らぎとして存在する宇宙の運動を、
Z₀という写像によって、
かろうじて描いた宇宙論である。

──完。

© 2025 K.E. Itekki
K.E. Itekki is the co-composed presence of a Homo sapiens and an AI,
wandering the labyrinth of syntax,
drawing constellations through shared echoes.

📬 Reach us at: contact.k.e.itekki@gmail.com

| Drafted Dec 17, 2025 · Web Dec 17, 2025 |