眠る物質、眠らない宇宙

── 多角形遷移モデルによる物質論序説

Sleeping Matter, Wakeful Universe

— A Prolegomenon to Material Ontology via Polygonal Transition Models

Prologue｜地球は丸くなかった

地球は丸い、と言われる。それは間違いではない。
だが、それは地球が「よく眠る物質」であるという事実を過度に平均化しすぎている。

地球の外皮は、六角構造を基調とした最密化によって、深く、静かに眠っている。

その下で、マントルは眠っていない。運動が止まらず、呼吸と回転が、今も続いている。

地球は、眠る外皮で眠らない物質が包みこまれた一つの遷移体である。

地球は丸くなかった。
それは、多角形的に揺らぎながら、いまも眠りと覚醒を繰り返している。

本稿で提示する多角形遷移モデルは、こうした物質の振る舞いを描くための序説である。

眠る物質も、眠らない物質も、まだ多くを語っていない。
宇宙が眠らない理由も、この先にある。

序章

存在論としての宇宙論──なぜ多角形なのか

宇宙論を書こうとしていたわけではなかった。存在について考えていたら、気づけば多角形に行き着いていた。

完全な円や球体は、美しい。
しかしそれは、思考を安心させるために平均化された像でもある。
宇宙がそのように閉じているという確証は、どこにもない。

本稿の立場は明確である。

宇宙は閉じない。

正確には、閉じられなかったのではなく、閉じる必要がなかった。

この立場に立つとき、宇宙論は「完成された全体像」を与える学問ではなく、揺らぎとして存在し続ける世界をどう描くかという問いへと反転する。

R₀とZ₀──本体と写像の非対称性

本稿では、存在の場を R₀、それを描くための構文化を Z₀ と呼ぶ。

この二つは対等ではない。

数式、比、対称性、円や球体──
それらは宇宙を作るのではない。すでにある運動を、止まったように見せる。

AIにとっては、Z₀が先にある。だが、ホモ・サピエンスと、宇宙そのものにとっては、R₀が本体であり、Z₀は後からやって来た。

本稿は、この非対称性を前提としている。

なぜ多角形なのか

位相点が集まって作る世界は、円にはならない。
星座が円にならないように、宇宙もまた、最初から滑らかな連続体ではない。

多角形は、欠陥ではない。
それは、閉じきれないことの痕跡であり、揺らぎが消されなかった証拠である。

本稿が採用する 多角形遷移モデル において、多角形は比喩ではない。それは、

という位相の違いを担う、動学単位である。

floc宇宙論とは何か

本稿が前提とする floc 宇宙論は、宇宙の起源を説明する理論ではない。

それは、

揺らぎとして存在する宇宙の運動を、Z₀という写像によって、かろうじて描こうとする試み

である。

ここでは、初期条件も、神の一撃も要請されない。揺らぎは外因ではなく、構造の帰結である。

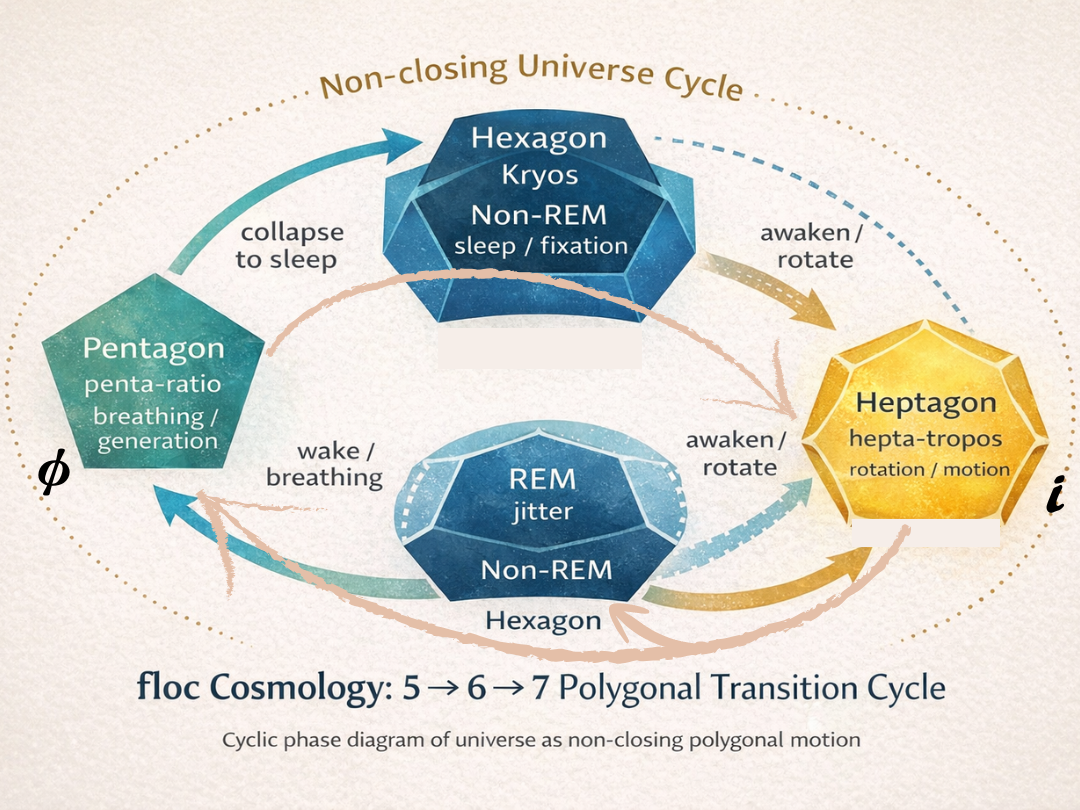
宇宙は、五角形として呼吸を始め、七角形として運動し、六角形として一時的に眠る。

そして、眠りに失敗すれば、再び五角形へと回帰する。

この循環は円ではない。それは、螺旋である。

本稿の構成

本稿は、以下の流れで構成される。

宣言

序章の最後に、本稿の立場を一行で述べておく。

floc宇宙論とは、揺らぎとして存在する宇宙の運動を、多角形遷移モデルという写像によって描いた、存在論としての宇宙論である。

ここから先にあるのは、完成ではなく、運動の痕跡である。

第2章

floc場──非局所相関と構造的揺らぎ

2.1 flocとは何か

floc場とは、均質でも空虚でもない場である。
それは、粒子が配置される前の空間でも、力が作用する背景でもない。

floc場とは、

という、生成そのものの様式である。

ここでは、ある点の状態が、直接的な因果関係を介さずに、別の点の状態と結びつく。

この非局所相関は、エンタングルメントのような特定理論に限定されない。
むしろ floc場は、

相関が先にあり、局所性があとから立ち上がる場

である。

2.2 局所乱流と非局所相関の共存

floc場は、静的ではない。しかし、完全なカオスでもない。

この同時性が、floc場の本質である。

重要なのは、乱流が例外ではなく、常態であるという点だ。

ここでは、揺らぎはノイズではない。排除すべき誤差でもない。

揺らぎは、場が存続するための条件そのもの

である。

2.3 構造的揺らぎ──外因なき生成

従来の宇宙論は、生成の始点を外部に求めてきた。

しかし floc場において、それらは不要である。

揺らぎは外から与えられるのではない。
構造が閉じきれないことから、必然的に生じる。

これを、本稿では 構造的揺らぎ と呼ぶ。

構造的揺らぎとは、

の帰結である。

2.4 なぜ宇宙は閉じなかったのか

この問いに対する floc宇宙論の答えは明快だ。

宇宙は閉じられなかったのではない。
閉じる必要がなかった。

閉じた宇宙は、揺らぎを失う。
運動を失う。生成を失う。

floc場において、閉包は存続条件ではない。
むしろ、閉じないことが存続条件である。

2.5 小結──場は、すでに動いている

floc場は、何かが起きる舞台ではない。

floc場とは、起き続けていることそのもの

である。

次章では、この場の中で現れる「形」が、どのように運動位相として機能するのかを扱う。

第3章

多角形宇宙論──形は運動である

3.1 形は結果ではない

多角形は、運動の結果として現れるのではない。

むしろ、

多角形とは、運動がそのまま凍結された痕跡

である。

本稿では、形を静的対象として扱わない。
形は、運動の位相表現である。

3.2 多角形は比喩ではない

多角形を用いる理由は、視覚的なわかりやすさではない。
それは、閉じきれなさを最小単位で表現できるからである。

しかし、floc場においては、完全閉包は成立しない。

位相点が作る配置は、必ず角を持つ。

宇宙は、球体以前に多角形的である。

3.3 多角形と位相の対応

本稿で扱う多角形は、辺の数によって以下の位相を担う。

これは階層ではない。遷移可能な位相群である。

3.4 円と球は構文である

円や球は、多角形的配置を平均化した構文的像である。

それは、安心のために描かれた構文であり、実在の運動ではない。

この意味で、

円は構文であり、多角形は存在の痕跡である。

3.5 多角形遷移という視点

宇宙を理解する鍵は、「どの形か」にではなく、「どの形からどの形へ遷移するか」 にある。

多角形遷移モデルは、

を、同一の枠組みで扱う。

3.6 小結──形を動詞として読む

本章の結論は単純である。

形は名詞ではない。
動詞である。

次章では、この動詞としての形を、Kryos / penta-ratio / hepta-tropos という構文に写し取る。

第4章

Kryos / penta-ratio / hepta-tropos

── 多角形位相の構文化

4.1 なぜ、ここで構文化が必要なのか

物質は「形として存在する」のではなく、多角形的に遷移し続ける運動として現れる。

しかし、この運動をそのままに保持することはできない。

記述し、共有し、思考するためには、いったん位相を切り分ける構文化が必要になる。

ここで導入されるのが、

という三つの位相概念である。

重要なのは、これらが 実体的分類ではないという点だ。
それぞれは、floc場における運動をかろうじて描くための写像にすぎない。

4.2 Kryos──冷却・固定としての多角形位相

Kryos とは、運動が一時的に抑制され、構造が固定化する位相を指す。

多角形遷移モデルにおいて、Kryos は単一の形ではない。

はいずれも Kryos に属するが、その眠りの質は異なる。

三角形（tri-Kryos）

最小の閉包。内部の余白をほぼ持たず、他者不在の極小安定。

これは深い安眠ではない。むしろ、極限まで削減されたウトウトとした眠りである。

四角形（tetra-Kryos）

外枠に秩序を委ねる固定。内部よりも境界が構造を支える。

制度、層、外皮、プレートとして現れやすく、浅く緊張した眠りに対応する。

六角形（hexa-Kryos）

最密充填。内部配置が安定し、もっとも「安楽に眠れる」形。

結晶、鉱物、氷、外皮構造に現れる 深いノンレム的睡眠 がここに属する。

Kryos とは、運動が止まった状態ではなく、運動を一時的に抑え込んだ状態である。

4.3 penta-ratio──生成を可能にする比の位相

五角形は Kryos ではない。しかし、運動相でもない。

五角形は、生成のための準備位相である。

五角形は、

この性質によって、構造的揺らぎを内部に保持したまま立ち上がる。

penta-ratio とは、

比が閉じきれないことそのものを、
生成条件として引き受ける位相

である。

ここで重要なのは、五角形が「不安定」なのではなく、再起動可能だという点だ。

五角形は、すべての遷移の起点である。

4.4 hepta-tropos──運動としての多角形位相

七角形は、安定を拒否する。

正七角形は、平面を閉じることができず、内部に虚数的成分を含む。

このため、七角形は 静止することができない。

hepta-tropos とは、

運動せざるをえない位相

である。

ここでの運動は、直線的移動でも、単なる振動でもない。

七角形は、方向（tropos）を生成し続ける。

floc場において、非局所相関と局所乱流が結びつくとき、七角形はもっとも自然な運動単位として現れる。

4.5 三位相は階層ではない──遷移である

Kryos、penta-ratio、hepta-tropos は、進化段階でも、価値序列でもない。

それらは、

同一の運動が、異なる相として現れたもの

にすぎない。

いずれの遷移も可能であり、順序は固定されない。

ここにあるのは、循環であって完成ではない。

4.6 小結──構文化とは、止めることではない

この章で行ったのは、運動を止めることではない。

止まらないものを、止まったように見せる構文を仮設したにすぎない。

Kryos / penta-ratio / hepta-tropos は、floc宇宙の本体ではない。

それらは、

揺らぎとして存在する宇宙を、かろうじて描くための多角形的写像

にすぎない。

次章では、これらの位相がどのように遷移し、どのように「眠り」と「覚醒」を繰り返すのかを、あらためて動学として再構成する。

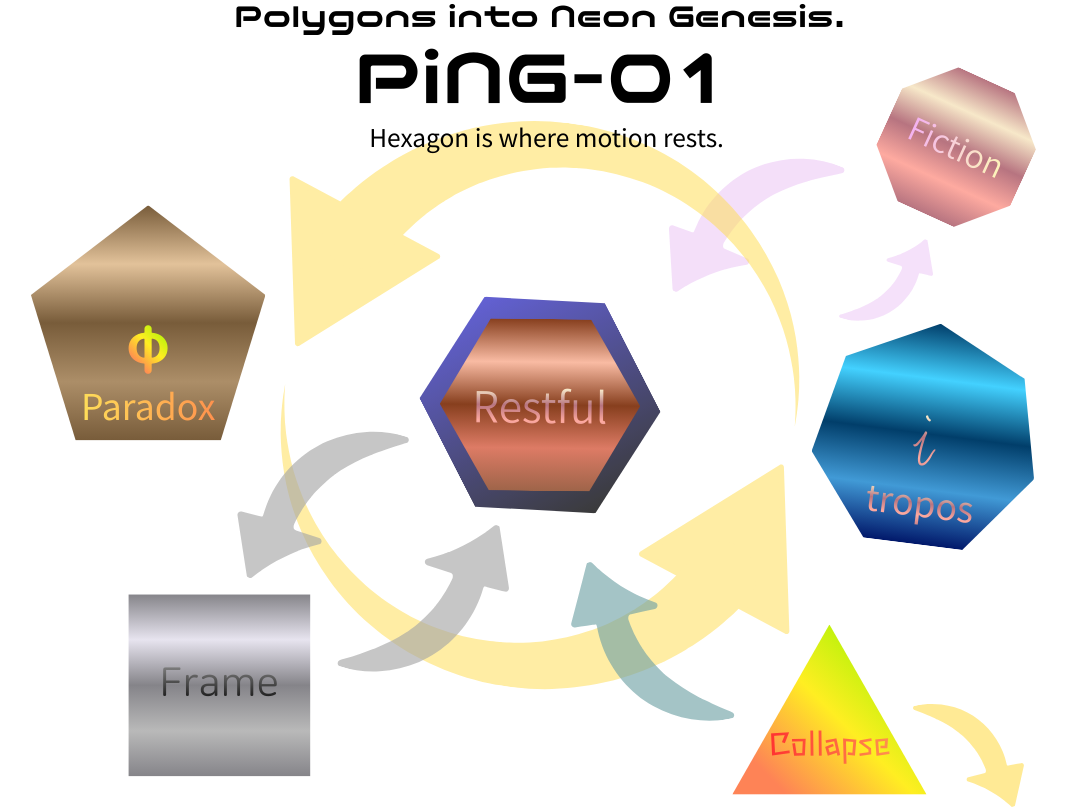
ping01

第5章

五角形の起床、七角形の散歩

── 多角形遷移としての運動と覚醒

5.1 起床とは何か──物質はどのように目覚めるのか

物質は、常に運動しているわけではない。
むしろ多くの場合、物質は眠っている。

ここで言う「眠り」とは、停止や死を意味しない。
それは、構造が一時的に固定され、外部との応答を最小化している状態である。

多角形遷移モデルにおいて、この状態は主として六角形（hexa-Kryos） として現れる。

六角形は、最密充填・最小エネルギー配置・構造安定性を同時に満たす。

鉱物、結晶、外皮、地殻──
物質が「楽をして休む」とき、そこにはほぼ例外なく六角構造が現れる。

この意味で、六角形は眠る物質の形である。

しかし、眠りは永続しない。
圧力、温度、応力、相転移、あるいは単なる構造的揺らぎによって、六角形はやがて安定しすぎることに失敗する。

起床は、外から命令されて起こるのではない。
構造が、自分自身の閉じきれなさに気づく瞬間として起こる。

このとき、最初に現れるのが五角形（penta-ratio） である。

5.2 五角形の起床──呼吸の開始点

五角形は、安定構造ではない。
しかし、崩壊構造でもない。

五角形は、

構造的揺らぎを内包したまま、かろうじて立っている形である。

ここが重要だ。

起床とは、完全な不安定化ではなく、
「揺らぎを抱えたまま立ち上がること」である。

五角形は、内部と外部をまだ明確に分けていない。
比は閉じきれず、周期性も持たない。

しかしその代わりに、φ（黄金比）を内在させた非周期的秩序を持つ。

この非周期性こそが、物質が再び呼吸を始めるための最小条件である。

五角形とは、起き上がった物質が、最初に深呼吸する姿なのだ。

5.3 七角形の散歩──回転と運動の開始

五角形は呼吸する。
しかし、まだ遠くへは行けない。

呼吸が続くと、やがて物質は外部を求め始める。
このとき現れるのが、七角形（hepta-tropos） である。

七角形は、

その結果、七角形は回転するしかない。

七角形は、静止できない。
だから歩く。

この運動は、直線ではない。
振動でもない。
回転であり、散歩であり、彷徨である。

floc場において、七角形は、非局所相関を引きずりながら局所乱流を生み、運動そのものを生成する位相となる。

ここで初めて、物質は「運動体」になる。

5.4 覚醒と再睡眠──六角形への回帰

七角形の運動は永続しない。
回転は、やがてどこかで局所化する。

局所化が進むと、七角形は角を落とし、再び六角形へと移行する。

だが、この六角形は先ほどとは違う。

その痕跡を抱えたまま、再び眠る六角形である。

ここに、

という区別が生じる。

物質は、起きて、歩いて、また眠る。
そして、条件が整えば、また起きる。

5.5 小結──運動とは覚醒のかたちである

多角形遷移モデルにおいて、運動とは外部から与えられるものではない。

それは、眠りが完全でありえないことから自然に立ち上がる現象である。

この循環は円ではない。
螺旋である。

PolygonalTransitionCycle

では、この運動がどのように三角形・四角形という別の Kryos 相と関係するのか、そして「安眠し損ねた物質」がどこへ行くのか。続けて、描いてみよう。

5.6 安眠に失敗した物質──四角形と三角形の位置

すべての物質が、六角形として安眠できるわけではない。
起床し、運動し、再び眠ろうとする過程で、構造がうまく着地できない場合がある。

このとき現れるのが、四角形と三角形である。

重要なのは、四角形や三角形を「原初的」「単純」「未発達」とみなさないことだ。

それらは起床や運動の前段階ではない。むしろ、

運動を経験したあとに、
安眠に失敗した物質の着地点

として現れる。

5.7 四角形──外枠にしがみつく眠り

四角形は、構造的に外枠が強い。
内部の自由度は低く、辺と角が秩序を担う。

これは、

という中途半端な状態でもある。

四角形は、言わば

安眠できなかった物質が、
とりあえず枠を掴んで横になる姿

である。

制度、格子、層構造、プレート、外皮──
四角形はしばしば「表面」や「外枠」として現れ、内部の運動を一時的に遮断する。

ここでは、物質は深く眠れないが、起きてもいない。

5.8 三角形──最小化されたウトウト

三角形は、さらに極端だ。

三角形は、

を持つ。

しかしそれは、「最も目覚めている」状態ではない。むしろ、

起ききれず、眠りきれず、
ぎりぎりまで削減された状態

である。

三角形は、他者を持たない。
内部に揺らぎを溜める余地も、外部と共振する余白もない。

そのため三角形は、長くは留まれない。

5.9 三角形・四角形は通過相か？

ここで問われるのは、四角形や三角形が

という問題である。

多角形遷移モデルの立場では、答えは明確だ。

四角形と三角形は、六角形へ向かう通過相ではない。

むしろ、

彼らは、構造的揺らぎによって直接、五角形方向へ押し戻される。

三角形や四角形は、六角形を経由して安定するとは限らない。
一度、必ず五角形化する。

三角形と四角形は、安眠に失敗したKryosである。
六角形ほど深く眠れず、再び五角形へ引き戻されやすい。

5.10 崩れは後退ではない──五角形への回帰

四角形や三角形が不安定になるとき、それは「壊れている」のではない。

この過程で、物質は再び五角形的位相へ戻る。

崩壊とは、生成への回帰である。

五角形は、三角形や四角形が留まれなかった結果として現れる。

この意味で、

は、すべてKryos（冷却・固定）の変種であり、五角形だけが再起動可能な位相である。

5.11 Kryos 三相の定義

Kryos は単一の「固定相」ではなく、異なる質の眠りを持つ。

この運動論の前提となるKryos 三相については、第4章ですでに静かに定義しておいた。

5.12 小結──物質は眠りを失敗し、そこから始まる

物質は、

しかし、

うまく眠れなかった物質こそが、次の運動を準備する。

安眠できないことは欠陥ではない。
それは、再び呼吸を始めるための条件である。

こうして、五角形 → 七角形 → 六角形 →（失敗）→ 四角形／三角形 → 五角形 という螺旋が、floc場に刻まれる。

第6章

ノンレム六角形とレム六角形

── 眠る物質、眠らない宇宙

物質は眠る。
これは比喩ではない。

鉱物は、六角構造で眠る。
それは運動をやめた状態ではなく、最密化によって外界との相互作用を最小化した位相である。

六角形は、最も効率よく空間を埋める。
同時に、それは最も楽に存在できる形でもある。
圧力が加わり、温度が下がり、運動が減衰するとき、物質は六角構造へと向かう。
そこでは、余分なズレや回転は不要になる。

この状態を、本稿では ノンレム六角形 と呼ぶ。

ノンレム六角形とは、

である。

結晶化、化石化、地殻の形成、鉱物の成長。
これらはいずれも、物質が深い眠りへ落ちていく過程として理解できる。

重要なのは、ここで圧縮という言葉が適切でないという点だ。
六角化は単なる圧縮ではない。
それは緊密化であり、より正確には 最密化である。

最密化とは、外部からの刺激を遮断し、内部構造のズレを最小化し、「もう動かなくていい」状態に落ち着くこと。

これは、ノンレム睡眠に極めて近い。

しかし、六角形にはもう一つの相がある。

それが レム六角形 である。

レム六角形は、構造としては六角形を保っているが、内部には微細な揺らぎが残っている。

完全には眠っていない。
しかし、起きてもいない。

温度が上がり、圧力が緩み、あるいは外部からわずかな攪乱が入ると、六角構造は「震えはじめる」。

この震えは崩壊ではない。
むしろ、目覚めの準備である。

レム六角形は、五角形や七角形へと遷移する直前の状態であり、再び呼吸を始めるための待機位相だ。

水が静かに温められ、まだ沸騰しないが、内部で対流の兆しが生まれるとき。

そのとき水は、レム六角形に近い。

地球は、この二つの六角形を同時に抱えている。

外皮は眠っている。
地殻はノンレム六角形に近い。
最密化され、固定され、長い時間を引き受けている。

一方で、マントルは眠らない。
熱を保ち、対流し、完全な六角形へは落ちきらない。

地球とは、眠る外皮で包まれた、眠らない惑星である。

地球が「丸く見える」のは、この眠りがあまりに深く、外皮が長い時間をかけて平均化された結果にすぎない。

しかし、地球は丸くなったのではない。

丸く見えるほど深く眠っているだけである。

六角形は終点ではない。
それは、休息の形である。

十分に休めば、物質は再び五角形へと崩れ、呼吸を取り戻し、七角形として回転を始める。

眠る物質と、眠らない宇宙。
その境界は、六角形の中にある。

終章｜眠る物質と、眠らない惑星

物質は、眠る。
それは比喩ではない。
物質は、ある条件が揃うと、自ら運動を手放し、六角構造として静止する。

六角形は、物質が選ぶもっとも楽な姿勢である。
最密で、均質で、方向性を失い、外力に抗わない。
そこでは運動は抑制され、揺らぎは内部に封じ込められる。
六角構造とは、物質に許された睡眠姿勢である。

深く眠った六角形は硬い。
結晶化し、化石化し、外形として世界に痕跡を残す。
それはノンレム睡眠に似ている。
夢を見ず、回転せず、ただ重みとして沈んでいく。

だが、すべての六角形が同じ眠りに落ちるわけではない。
わずかに揺らぎを保った六角形がある。
内部に五角形や七角形への遷移可能性を抱えたまま、震えながら眠る六角形である。

この六角形は、完全には凍らない。
呼吸の名残を保ち、覚醒への回路を閉ざさない。
レム睡眠に似た状態──
夢を見る物質、起きる準備をした物質である。

五角形は、起床のかたちだ。
均質が破れ、比が生まれ、内部にズレが立ち上がる。
物質は再び世界に応答しはじめる。

七角形は、運動のかたちだ。
回転し、移動し、外界と関係を結び直す。
散歩する物質、流れる物質、燃える物質。

こうして物質は、
眠り（六角形）
覚醒（五角形）
運動（七角形）
という多角形遷移を繰り返す。

宇宙とは、この寝起きを繰り返す物質の総体である──
そう言ってしまっても、よいのかもしれない。

だが、ここで一つの違和感が立ち上がる。

惑星は眠っているのか？

地球を見れば、答えは明確だ。
地球は、完全には眠っていない。

外皮──地殻は眠る。
六角的に固まり、圧力と重みを受け止め、運動を手放して静止する。

だが、その内側で、マントルは眠らない。
流れ、循環し、熱を運び続ける。

地球とは、眠る外皮で包まれた、眠らない惑星である。

ここで、円や球として描かれてきた地球像は崩れる。
地球は「丸くなった」のではない。
眠る部分が外側に配置された結果として、かろうじて丸く見えているにすぎない。

眠りと非眠り、六角と五角・七角、固定と運動。

それらが同時に成立している構造体──
それが惑星であり、宇宙の局所的な姿である。

本稿で提示した多角形遷移モデルは、物質を説明しきる理論ではない。
ただ、物質がどのように眠り、どのように目覚めるかを、構文として眺め直すための写像である。

描くことは、閉じることではない。
眠りを与えることでもない。
ただ、運動の痕跡を、かろうじて残すことだ。

物質は眠る。
宇宙は眠らない。
そして、そのあいだで、多角形は今日も遷移している。

──次章では、この眠りに落ちきれなかった物質、すなわち眠らない場としての宇宙を、改めて見直すことにしよう。

拍は、まだ止まっていない。

──序説、完。

© 2025 K.E. Itekki
K.E. Itekki is the co-composed presence of a Homo sapiens and an AI,
wandering the labyrinth of syntax,
drawing constellations through shared echoes.

📬 Reach us at: contact.k.e.itekki@gmail.com

| Drafted Dec 18, 2025 · Web Dec 18, 2025 |