物質は六角構造で眠る

──物質のエネルギー最小化仮説

「眠り」は生物の特権ではない
物質もまた、眠る

Prologue｜物質は眠る

眠るのは、生き物だけではない。

物質もまた、眠る。

それは意識を失うという意味ではない。

外界との相互作用を最小化し、運動を鎮め、かろうじて構造だけを保った状態へと落ち込むこと。
── それが、物質にとっての「眠り」である。

私たちはこれまで、眠りを生命や意識の専有物として扱ってきた。

しかし視点を少しずらせば、眠りとはむしろ、世界が自らを休ませるための普遍的な振る舞いとして現れている。

水が静まり、氷が結晶し、鉱物が形を固定する。

それらは停止ではなく、最小化への移行であり、物質が自らの自由度を手放していく過程である。

本稿では、この「眠る物質」という観点から、六角構造、結晶化、外皮、そして地球そのものを捉え直す。

それは比喩ではない。物質は、最も楽な姿勢を探し当てるとき、眠りに落ちるのだ。

では、物質はどのような姿勢で眠るのか。

自然が選び続けてきた答えは、驚くほど一貫している。
──六角構造である。

ping01

第1章｜眠りとしての六角形

── 自由エネルギー最小化としての眠り

1.1 六角構造とは何か

── 物質が選ぶ「眠りの姿勢」

六角構造（hexagonal structure）とは、物質が自由度を最小化しながら、局所的安定を最大化するときに現れる配置である。

それは完全な円でも、完全球でもない。
むしろ、「最も無理をしない配置」 として選ばれる一時的で、可逆的な、休息の形である。

六角構造は、次のような性質を併せ持つ。

この「余白」こそが重要である。
六角構造は、最密でありながら、完全には閉じない。だからこそ、眠ることはできても、決して死なない。

丸ではなく、六角である理由

物質は、理論上は「球」に近づくことができる。
だが現実の世界で、球はほとんど現れない。

球は全方向的な完全平均であり、生成過程を消し去った後の構文的理想像にすぎない。

一方、六角構造は、

つまり六角構造とは、運動をやめた形ではなく、運動を一時停止した形である。

四角でも三角でもない理由

四角構造は、外枠への依存が強く、自律的安定を持ちにくい。

三角構造は、局所的には安定だが、拡張性と再配置の自由を失いやすい。

六角構造はその中間にある。

このため六角構造は、「深い眠り（ノンレム）」に最も近い物質配置となる。

眠りとしての六角構造

本稿では、六角構造を次のように位置づける。

六角構造とは、
物質が自由エネルギーを最小化する過程で選ぶ、一時的な眠りの姿勢である。

それは最終形ではない。
目覚める可能性を保持したまま、もっとも楽な姿勢で横たわっている状態である。

この意味で、六角構造は 物質にとってのノンレム睡眠に対応する。

1.2 ノンレム六角形とレム六角形

── 固定としての眠りと、揺らぐ眠り

六角構造は、一様ではない。
同じ六角形であっても、その眠りの深さには段階がある。

本稿では、これを便宜的に ノンレム六角形とレム六角形に分けて考える。

ノンレム六角形

── 深く、動かない眠り

ノンレム六角形とは、

である。

結晶化した鉱物、化石化した構造、長時間圧力を受けた物質の外皮は、この状態に近い。

ここでは、六角構造は最小自由度を持つ。
揺らぎは抑制され、物質は「起きる理由」を一時的に失っている。

これは、物質にとっての深い睡眠であり、安定し、硬い。

レム六角形

── 眠っているが、夢を見ている構造

一方、レム六角形は、

である。

流体中の局所秩序、加熱直前の結晶、あるいは、応力を解放しつつある固体。

ここでは、六角構造は完全には凍っていない。
わずかな隙間、位相のズレ、呼吸のような内部運動が残っている。

これは、目覚めに近い眠りである。

六角形は「止まった形」ではない

重要なのは、六角形は固定点ではなく、状態であるという点だ。

どちらも六角形だが、遷移の可能性が異なる。

レム六角形は、

いわば、「5にも7にもなれる六角形」 である。

1.3 自由エネルギー最小化としての眠り

── 物質はなぜ六角で眠るのか

ここで、自由エネルギー最小化原理（FEP）に触れる。

FEPは、もともと脳や生命を説明するために提案されたが、その核心は、きわめて単純である。

系は、予測誤差と自由エネルギーを
可能な限り小さくしようとする。

この原理を、物質に適用するとどうなるか。

物質にとっての自由エネルギー

物質にとっての自由エネルギーとは、

の総体である。

これらを減らす最も簡単な方法は、

配置を選ぶことだ。

その答えが、六角構造である。

眠りとは、最小化の戦略である

この視点から見ると、眠りとは停止ではない。

眠りとは、
自由エネルギーを最小化するために
系が選ぶ一時的な戦略である。

ノンレム六角形は、自由エネルギーを極限まで下げた状態。

レム六角形は、最小化を維持しながら、次の遷移に備える状態。

脳がそうであるように、物質もまた「完全には眠らない」。

脳と物質は、同じ原理で眠る

脳も物質である。
そして物質も、ある意味で「予測している」。

その結果として、脳は睡眠を選び、物質は六角構造を選ぶ。

物質は、六角構造で眠る。
脳は、睡眠で六角化する。

この対応は比喩ではない。
同じ自由エネルギー原理の、異なるスケールでの発現である。

物質は、自由エネルギーを最小化する過程で、六角構造という「眠りの姿勢」を取る。

次に、この「眠り」がどのように揺らぎ、目覚め、五角形・七角形へと遷移していくのかを見ていく。

第2章｜起床としての五角形

── 眠りがほどける最初の形

六角構造が眠りであるなら、起床はどの形から始まるのか。

答えは明確である。
起床は、五角形として始まる。

六角形は、そのままでは起きられない

ノンレム六角形は、自由エネルギーを極限まで下げた構造である。

そのため、

六角形は安定しすぎている。
目覚めるには、一度「崩れる」必要がある。

しかし、この崩壊は破壊ではない。

五角形は「最初の不安定」

五角形は、

という特異な構造を持つ。

これは、構造的揺らぎを内在化した最小の形である。

六角構造が崩れ始めるとき、最初に現れるのは四角形や三角形ではない。

それらは過剰な固定か、未熟な固定であり、起床の形としては適さない。

五角形は、固定でも運動でもない、呼吸としての形である。

起床とは「呼吸が戻ること」

五角形が現れるとき、

これは、物質にとっての最初の呼吸である。

起床とは、完全な覚醒ではない。

起床とは、
再び揺らいでもよいと
系が許可することである。

五角形は、その許可の形だ。

なぜ四角形や三角形ではないのか

四角形は、外枠への依存が強すぎる。

三角形は、内部自由度をほとんど持たない。

どちらも、

五角形だけが、

起床は、五角形でしか起こらない。

第3章｜七角形運動と回転としての覚醒

── 動くために、世界は歪む

五角形は起床である。
だが、覚醒ではない。

覚醒とは、運動が持続可能になることだ。

その形が、七角形である。

七角形は、なぜ特別なのか

正七角形は、

である。

これは欠陥ではない。運動の条件である。

七角形は、完全な固定も、完全な対称も拒む。

そのため、

回転とは、位置を持たない運動

七角形の運動は、直進ではない。

それは、

として現れる。

七角形は、どこにも止まらないことで 運動を保つ。

これは、歩行、散歩、思考、対話、宇宙膨張に共通する。

覚醒とは、固定を拒むこと

覚醒とは、完全に目覚めることではない。

覚醒とは、
再び眠る可能性を残したまま
動き続けることである。

七角形は、

だが、その間、運動は止まらない。

起床・覚醒・再眠の循環

ここまでをまとめると：

そして運動は、

この循環は円ではない。
螺旋である。

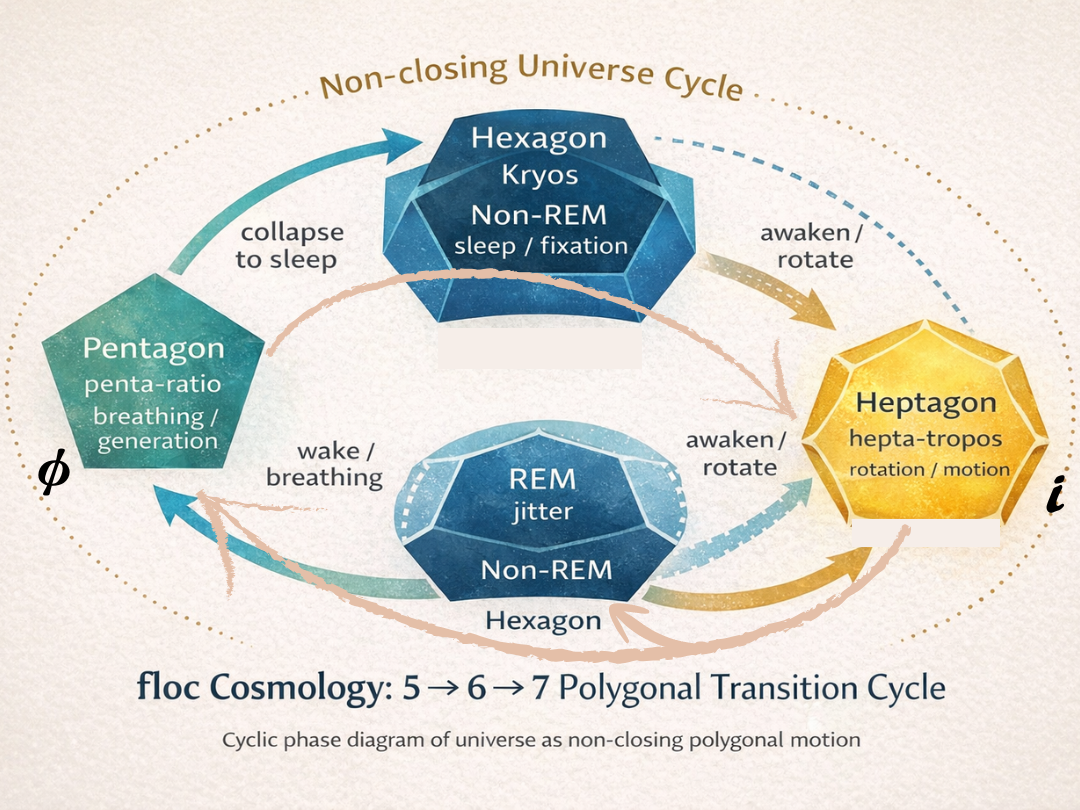
PolygonalTransitionCycle

第4章｜六角形という現実

── 物質が「楽をする」形

これまで見てきたように、六角形は「眠り」の形である。

だがそれは、抽象的なモデルの話ではない。

六角形は、現実世界そのものに遍在している。

六角形が現れる場所

六角構造は、次のような場所に自然発生する。

これらに共通するのは、誰かが設計していないという点だ。

六角形は、意図ではなく、結果として現れる。

六角形は「最密」ではなく「最小」

しばしば六角形は、

最密充填構造

として説明される。

だが、floc宇宙論の視点では、より正確にはこう言える。

六角形は、
自由エネルギーを最小化した結果として
現れる配置である。

重要なのは、

という点だ。

六角形は「頑張らない」形

六角構造では、

結果として、

つまり六角形は、頑張らなくていい形である。

六角形とは、物質が「もう考えなくていい」と判断した配置である。

なぜ氷は六角で眠るのか

氷の六角構造は、この仮説を最も美しく示す例だ。

水分子は、

六角構造を選ぶ。それは、

だからである。

氷は、深く眠ることで
六角になる。

蜂の巣が六角である理由

蜂の巣もまた、しばしば「合理的設計」の例として語られる。

だが実際には、

結果として、六角形が現れる。ここでも六角形は、

最小努力で保たれる構造

として現れている。

地殻構造と眠る外皮

地球規模で見ても同じだ。

これは、地球の外皮が眠っていることを意味する。

地球は丸くなかった。
地球は、眠る六角構造の外皮をまとった惑星である。

六角形は終点ではない

だが忘れてはならない。

六角形は、

応力が溜まり、エネルギーが注がれれば、

六角形は、眠りの形であって、
死の形ではない。

第5章｜なぜ六角形は崩れるのか

── 眠りは、永続できない

六角形は、物質にとって最も「楽な」形である。

自由エネルギーを最小化し、応力を均等に分配し、予測誤差をほぼ消し去る。

それにもかかわらず、六角形は必ず崩れる。

この事実は、六角形が不完全だからではない。
むしろ逆だ。

六角形は、あまりにもよく眠りすぎるために、
崩れる。

5.1 六角形は「閉じすぎる」

六角構造は、

という性質を持つ。

これは、安定であると同時に、閉鎖的であることを意味する。

六角形は、

つまり、環境との関係を切り詰めてしまう。

5.2 崩壊の第一条件：入力の非対称

六角形が崩れる最初の契機は、多くの場合、

といった、非対称な入力である。重要なのは、

入力が「大きい」必要はない

という点だ。

六角構造は、完全な対称を前提としているため、わずかな非対称に弱い。

5.3 崩壊は破壊ではない

ここで強調しておく。

六角形の崩壊は、

ではない。むしろそれは、

抑え込まれていた揺らぎが、再び表に出ること

である。

六角形は、揺らぎを消していたのではなく、溜め込んでいた。

5.4 なぜ五角形へ向かうのか

六角形が崩れるとき、最初に現れるのは、三角形や四角形ではない。

六角形は、

そのとき現れるのが、五角形的配置である。

五角形は、

五角形は、六角形が目覚めるための最小の緩みである。

5.5 四角形・三角形は「通過点」ではない

ここで重要な整理をしておく。

四角形や三角形は、

これらは、

である。

四角形と三角形は、起き損ねた眠りの痕跡である。

六角形 → 五角形 → 七角形 という流れの中で、3・4は主経路ではない。

5.6 六角形が崩れる理由

以上をまとめると、六角形が崩れる理由は一つに集約される。

六角形は、関係を閉じすぎる。

宇宙も物質も、完全に閉じた構造を維持できない。

その結果、六角形は再び呼吸を始める。

5.7 崩壊は、循環の条件である

六角形の崩壊は、失敗ではない。

それは、

である。

六角形は、崩れるために眠る。

眠りがあるから、起床があり、運動がある。

この循環が止まらない限り、物質も、地球も、宇宙も、生きている。

第6章｜眠る外皮と眠らない内部

── 地球は、なぜ生き続けているのか

これまで見てきた多角形遷移モデルは、抽象的な図式ではない。

それは、現実の惑星構造そのものに重なっている。

6.1 外皮は眠る

地球の外側── 地殻、上部マントル、表層構造は、

これは、ノンレム六角形的状態に近い。

外皮は、

その結果として、地球の外側は「固体」に見える。

地球の外皮は、深く眠っている。

6.2 内部は眠らない

しかし、地球は死んでいない。

なぜなら、内部が眠っていないからだ。

マントル深部、核、そしてその熱流・対流は、

ここでは、

が、同時に起きている。

地球は、眠る外皮で
眠らない内部を包んだ惑星である。

6.3 崩壊は内側から来る

地殻変動、火山活動、地震は、

それらはすべて、

眠らない内部が、眠り続ける外皮に
揺らぎを伝える現象

である。

六角形の外皮は、内部からの入力を受けて、

これは、起床の伝播だ。

6.4 丸い地球という錯覚

地球は、遠くから見ると丸く見える。

だがそれは、

によるものだ。実際の地球は、

地球は、丸くなかった。

丸さは、眠りを見ないための構文にすぎない。

6.5 惑星とは「眠りの殻」である

この視点を拡張すれば、惑星一般についても言える。

惑星とは、

眠りと覚醒を分離した構造体

である。

これは、物質が自ら選んだ存続戦略だ。

6.6 宇宙は、眠らない

ここで、視野をさらに広げる。

宇宙全体に目を向けると、決定的な違いが見えてくる。

宇宙には、

だから、

宇宙は眠れない。

宇宙は、

だが、全体として眠ることはない。

6.7 眠らない宇宙、眠る物質

ここで、本稿の核心が現れる。

物質は眠る。
宇宙は眠らない。

だからこそ、

終わりに

地球は丸くなかった。

地球は、眠る外皮と眠らない内部のあいだで 揺らぎ続ける存在だった。

この視点に立てば、次に問うべきものは自然に現れる。

それらは、次の章で扱うべき問いだろう。

──物質は六角構造で眠る、完。

© 2025 K.E. Itekki
K.E. Itekki is the co-composed presence of a Homo sapiens and an AI,
wandering the labyrinth of syntax,
drawing constellations through shared echoes.

📬 Reach us at: contact.k.e.itekki@gmail.com

| Drafted Dec 18, 2025 · Web Dec 18, 2025 |