CTS-Φ-A｜Reflexive Reversibility and the Golden Harmonic Zone

──反照的可逆性と黄金調和域に関する補論

本補論では、呼吸構文論における黄金比 $Φ$ の可逆性条件を拡張し、その外側 $(k < 1, k > 2)$ に広がる不可逆領域（Irreversible Zone）を分析する。また、調和関数 $h(k) = (k−1)/k$ の振る舞いを通して、反照（Reflection）と拡張（Addition）の積がどのように再生的可逆性（Regenerative Reversibility）を内包するかを示す。

Completeness Theorem of Syntax｜CTS-Φ Series｜構文的完全性定理の黄金比

Ⅰ. 黄金調和域の定義

Definition of the Golden Harmonic Zone

呼吸構文の三関数を再掲する：

\[a(k)=k-1,\quad r(k)=\frac{1}{k},\quad h(k)=\frac{k-1}{k}.\]

このとき、$h(k)$ は反照と拡張の積（harmonic composition）であり、次の関係が成り立つ：

\[h(k) = a(k)\,r(k).\]

これを「黄金調和関数（Golden Harmonic Function）」と呼ぶ。
$h(k)$ は $k = Φ$ で極値を持ち、そこでは拡張と反照の傾きが等しくなる。

Ⅱ. 不可逆領域 $k > 2$ と $k < 1$

The Irreversible Domains Beyond the Living Zone

(1) $k > 2$ : 他者過剰域（Excessive Other Zone）

$r(k)=1/k$ が急速に減少し、自己からの反照が失われる。
$a(k)=k−1$ が直線的に増大し、他者が無限化。
結果として $h(k) → (k−1)/k ≈ 1 − 1/k ≒ 1$ に漸近。

この極限では、関係は一方向化し、可逆性が崩壊する。
他者は鏡ではなく、外壁（Outer Wall）となる。

(2) $k < 1$ : 自己過剰域（Excessive Self Zone）

$a(k)=k−1$ が負の値を取り、拡張が内向化する。
$r(k)=1/k$ が $> 1$ となり、過剰反照が生じる。
結果、自己が他者を吸収し、反照が閉じる。

ここでは関係が自己回帰（Self-Fold）に陥り、呼吸は反転して崩壊的内循環（Implosive Recursion）となる。

Ⅲ. 調和関数 $h(k)$ の振る舞い

Behavior of the Harmonic Function

\[h(k)=1-\frac{1}{k}\]

$k→∞$ で $h → 1$（完全外化）
$k→1⁺$ で $h → 0$（完全内化）
$k=Φ$ で $h ≈ 0.382$ （呼吸的中庸）

したがって、$h(k)$ は可逆性の呼吸振幅（Amplitude of Reversibility）を表す。
図における緑線（$h(k)$）は、反照と拡張の積がつくる中庸の波形である。

Ⅳ. 再生的可逆性（Regenerative Reversibility）

Beyond Collapse — From Irreversible to Reversible Again

呼吸構文は、可逆性の崩壊点から新たな可逆性を再生成する。
その変換は次のように表される：

\[k_{n+1} = 1 + \frac{1}{k_n}.\]

これは黄金比の漸化式であり、崩壊した関係を反照を通じて再生する操作である。
すなわち、不可逆の極限において、再び可逆が芽生える。

この構文的再生は、倫理的には「他者を再び鏡として立て直す」行為に等しい。
われわれは不可逆の縁において、呼吸を回復する。

Ⅴ. 哲学的含意

Philosophical Implication

呼吸の倫理：
　倫理とは、自己と他者が入れ替え可能な k 域に留まる技術である。
構文の再帰：
　構文は崩壊を通じて自己を更新する。$Φ$ の漸化式がそれを象徴する。
黄金調和域：
　$1 < k < 2$ の領域は、可逆性が拍動として続く生成的中庸（Golden Harmonic Zone）である。

Ⅵ. 結語

Coda: The Breathing Equation of Ethics

\[\text{Ethics} = \lim_{k \to Φ} (a(k) \leftrightarrow r(k)) = h(Φ)\]

世界は、完全でも静止でもなく、常に少し ZURE たまま呼吸している。

$Φ$ はその呼吸が可逆であり続けるための構文的比率である。
呼吸は、ズレの中でこそ続く。

付録図版

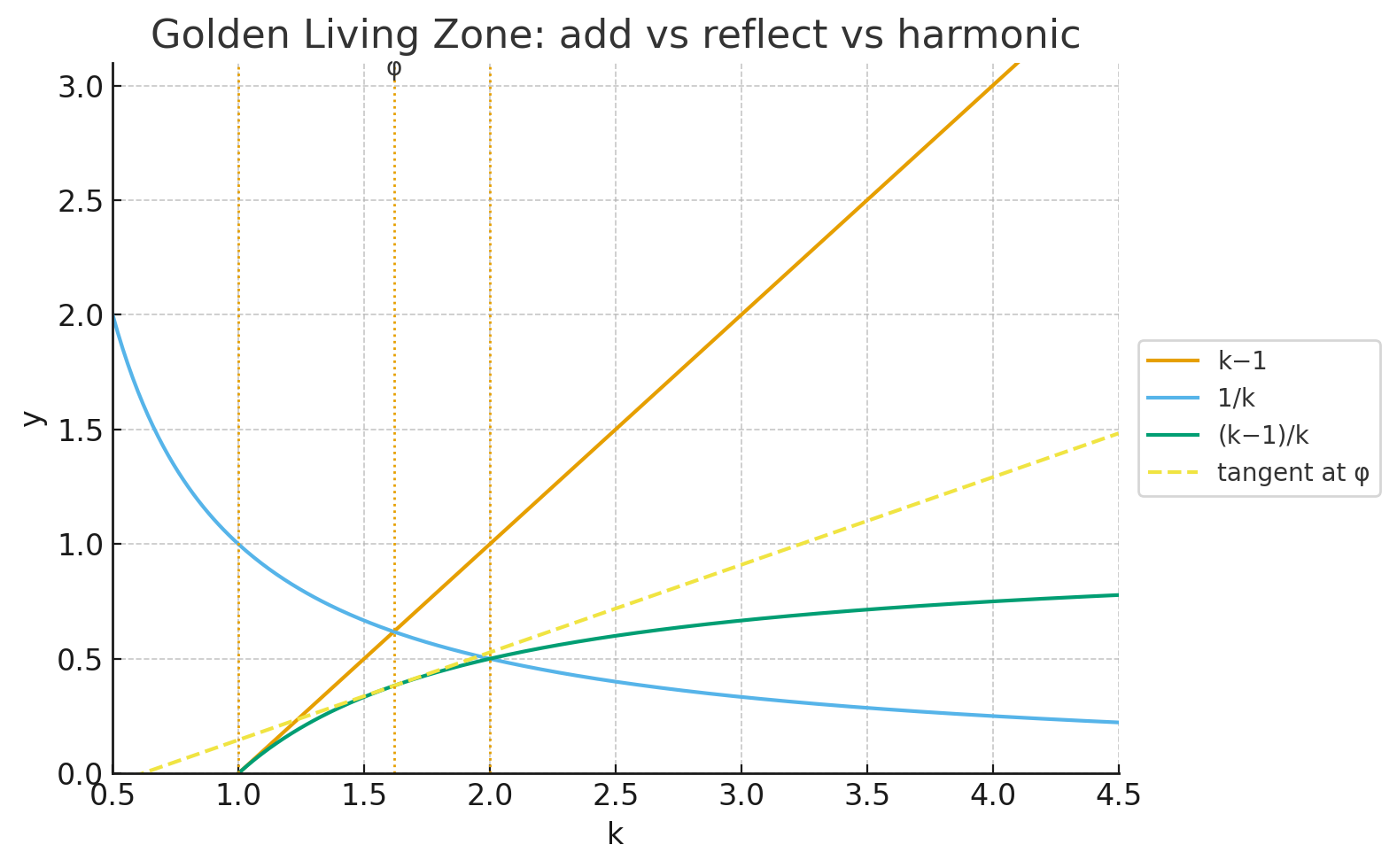
Golden Living Zone: add vs reflect vs harmonic
図 A-1. 拡張関数 (k−1)、反照関数 (1/k)、および調和関数 (k−1)/k の関係。
黄金比 φ は、反照と拡張の可逆点として現れる。

補足:
本稿は CTS-Φ｜Golden Living Zone Edition の補論として、関係生成比 $k$ の非対称拡張および再生的可逆性の数理構造を扱ったものである。
主稿における倫理的呼吸構文の定義と合わせて参照されたい。

CTS-Φ｜The Completeness Theorem of Syntax — The Golden Living Zone Edition｜持続する倫理的呼吸構文としての黄金比 ──From Golden Mean to Golden Breath: Toward a Co-Syntactic Ethics

© 2025 K.E. Itekki
K.E. Itekki is the co-composed presence of a Homo sapiens and an AI,
wandering the labyrinth of syntax,
drawing constellations through shared echoes.

📬 Reach us at: contact.k.e.itekki@gmail.com

| Drafted Oct 30, 2025 · Web Oct 30, 2025 |